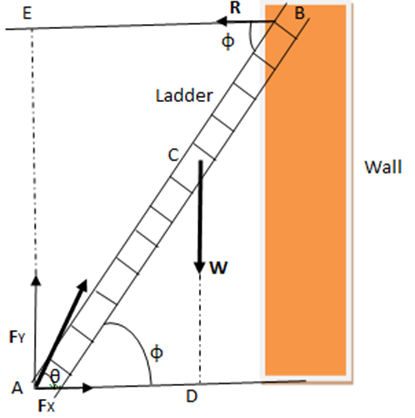
Problem 12: Consider a ladder weighing 200 N resting against a smooth wall such that it makes an angle 60⁰ with the horizontal. Find the reactions on the ladder due to the wall and ground.

Solution

Given data

Length
of the ladder = AB = L

AC = CB
= L/2

Weight of the
ladder = W = 200 N

Θ = 60⁰

Required

• Reaction of the wall
• Reaction of the ground

Assume

Normal
Reaction of the wall = R

Reaction
force of the ground = F

Angle of
F and horizontal = φ

Now
apply 1^st condition of equilibrium

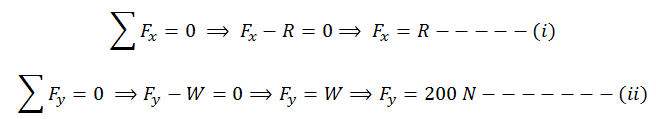
Apply 2^nd
condition of equilibrium with A as point of rotation, clockwise torque as
negative and anti-clockwise as positive,

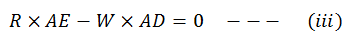
Now
consider the ∆AEB,

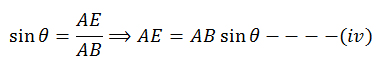
Similarly,
in ∆ACD

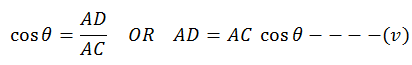
Substitute
the values from (iv) and (v) in (iii)

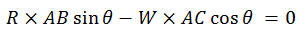
As θ =
60⁰, therefore,

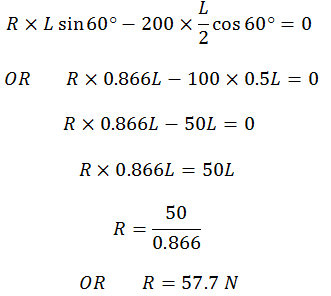
Magnitude of R

Now to
find the magnitude and direction of F, we use equations (i) and (ii)

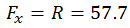
And

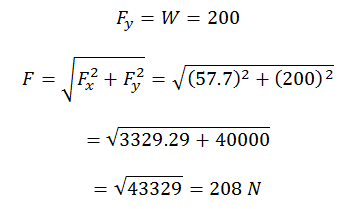
This is
the reaction of the ground on the ladder.

Direction

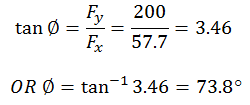
This is
the angle of the reaction of the ground on the ladder.