Problem 3: A ball of mass ‘m’ tied to one end of a string and is whirled from the other end in a vertical circle of radius ‘r’ with constant speed. Find out the tension in the string when the ball is at
(a) the highest point (b) the lowest point
Solution
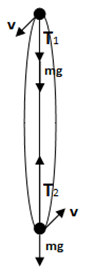
Theory: The ball is moving in a vertical circle. The gravitational pull on the ball during the course of motion is not uniform. When the ball is at the highest point, both tension in the string and weight of the ball is acting towards the center of the circle. When it is at the lowest point, tension in the string is acting upward and weight of the ball downward.
Given Mass of the ball = m Radius of the circle = r
Required Tension in the string at the highest point = T1 =?
Tension in the string at the lowest point = T2 =?
(a) Now when the ball is at the highest point, the net force on the ball = T1 + mg. This force provides the necessary centripetal force
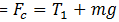
Put the value of the centripetal force
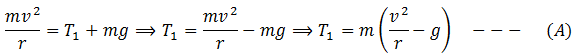
(b) When the ball is at the lowest point, the net force on the ball = T2-mg
Now this force provides the necessary centripetal force. Therefore,

Equations (A) and (B) give the respective values of tension in the string at the highest and lowest points.

Pingback:numerical-problems-on-circular-and-rotatory-motion-chapter-4-physics-11 – msa
Pingback:Calculate centripetal acceleration of the moon – msa