Problem 9: Show that when a hoop rolls down on an inclined plane, half of K.E is rotational and the other half is translational.

Solution

Theory: Again we use the theory that as the hoop falls down; it loses P.E which is converted to the K.E of the loop. The K.E thus gained is partly linear and partly rotational. According to the law of conservation of energy, Loss in P.E = Gain in K.E. This implies (P.E)_lost = (K.E)_lin + (K.E)_rot     ——     (1)

Now consider the adjacent figure. (Sorry, the drawing must be a daunting one!). The hoop of mass ‘m’ is falling down the incline and its P.E is converting to its K.E (linear + rotational). Using equation (1),

But we know that for a hoop,

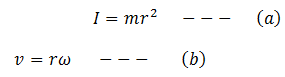
Put (a) and (b) in the above equation

Now simplifying

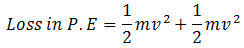
This equation shows the P.E is equally converted to linear K.E and rotational K.E. So half of the K.E is linear and half of it is due to rotational motion of the hoop.