Problem 4: Using the following data, draw a velocity-time graph for a short journey on a straight road of a motorbike.
| Velocity | 0 | 10 ms-1 | 20 ms-1 | 20 ms-1 | 20 ms-1 | 20 ms-1 | 0 |
| Time | 0 | 30 sec | 60 sec | 90 sec | 120 sec | 150 sec | 180 sec |
Use the graph to calculate
- the initial acceleration (b) the final acceleration (c) the total distance
Solution
The journey of the bike can be divided into 3 parts.
- Its velocity increases from 0 to 20 m/s in 60 sec.
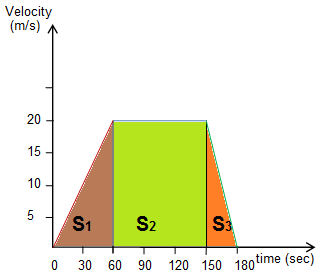
It is the case of increasing acceleration. The acceleration can be found by using, vf = vi + at. Put the values,
20 = 0 + a× 60 OR 20 = 60 a OR a = 20/60
OR a = 0.33 m/s … (1)
This equation gives the initial acceleration of the bike.
- 60 seconds onward, the bike goes with constant velocity for another 90 seconds, and therefore, the acceleration is zero during this interval of time. Therefore, a = 0 … (2)
- Now, after 150 seconds, the bike decelerates and comes to rest after 30 seconds. Therefore, during this interval of time, vi = 20 m/s, vf = 0 m/s, t = 30 sec. To find the acceleration, we apply the equation of motion, vf = vi + at. Put the values, 0 = 20 + 30a OR 30a = -20 OR a = -20/30 OR a = – 0.666 = -0.67 m/s2. … (3)
The negative sign shows the velocity decreases and this gives the final acceleration of the bike.
Total distance covered: The total distance the bike covers can be calculated by the three areas of the graph; 2 triangles and one rectangle. It is given by,
s = ½ (20 × 60) + (20 × 90) + ½ (30 × 20) = ½ × 1200 + 1800 + ½ × 600 = 600 + 1800 + 300 = 2700 m = 2.7 km

Pingback:numerical-problems-force-and-motion-chapter-3-physics-11