Problem 5: Four coplanar forces act on a body at a point O as shown in figure. Find their resultant.

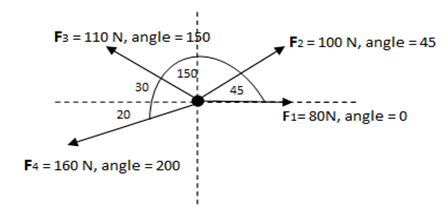
Solution

Strategy: Simply add the forces and get the resultant. The method should be adding by rectangular components. Find the x-components of all the forces and get the x-component of the resultant force by adding them up. Then find the y-components of all forces and sum up them to get the y-component of the resultant force. Once you have the x and y-components of the resultant force, use them to find the magnitude and direction of the resultant force.

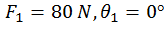
Therefore,

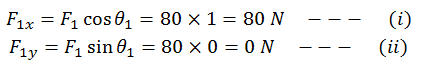
Also

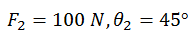
Therefore,

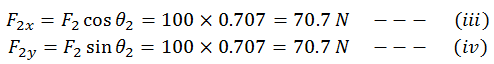
And

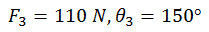
Therefore,

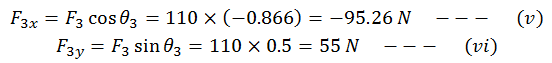
And

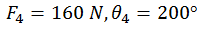
Therefore,

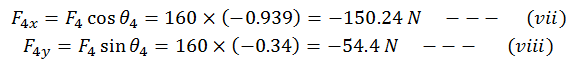
Add all the x-components to get the x-component of
the resultant. Hence adding (i), (iii), (v) and (vii) we have,

Fx = 80+70.7-95.26-150.24 = -94.8 N     —–    
(A)

Now add all the y-components to get the y-component
of the resultant force. Therefore, adding (ii), (iv), (vi) and (viii)

Fy = 0+70.7+55-54.4 = 71.3 N               ——     
(B)

Magnitude of the resultant

Magnitude of the resultant force is given by

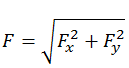
Did you know? If you have to find the value of n number of variables, you would need at least the same number of equations as the number of variables.

Put the values
from (A) and (B),

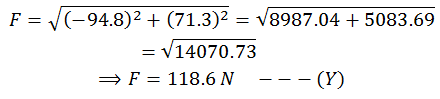
Direction of the Resultant

The direction of the resultant force can be
determined by

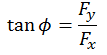
Put the values from (A) and (B)

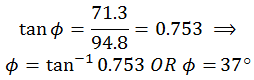
As the x-component is negative and y-component is
positive, the resultant is in the second quadrant. So the angle for the
resultant force is

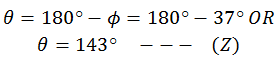
Equations (Y) and (Z) give the magnitude and
direction of the resultant force.