Problem 5: Eight equal drops of oil are falling through air with a steady velocity of 0.1 ms-1. If the drops recombine to form a single drop, what would be the new terminal velocity?
Solution
Given No of oil drops = 8, Terminal (steady) velocity of each drop = 0.1 ms-1
Required Terminal velocity of the single combined drop =?
Formula
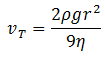
Theory As the oil drops have uniform density and equal size, the mass and volume of the combined drop will be eight times more than the individual droplets.
- Combined mass = M = 8m
- Combined volume = V’ = 8V
However, the radius of the combined drop will not be equal to 8 times the radius of the individual drops. The reason is volume and radius are not linearly (simple) proportional to one another. But volume is proportional to the cube of the radius.
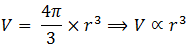
Therefore, if V is volume of the single droplet and r is its radius and V’ is the volume of the combined drop and R is its radius, then
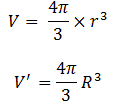
Since V’ = 8V, therefore,
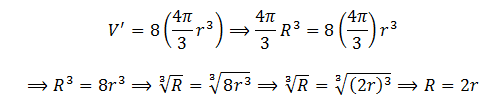
So to find the terminal velocity of the combined drop, we put this value of R in the formula.
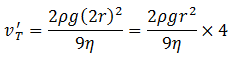
Put the value of the terminal velocity of the individual drop on RHS,

This is the terminal velocity of the combined drop.
Did you note the bigger drop moves faster than the smaller ones?

Pingback:numerical-problems-on-fluid-dynamics-chapter-6-physics-11