A cylinder of 50 cm diameter at the top of an incline 29.4 cm high and 10 m long is released and rolls down the incline. Find the linear and angular speed at the bottom. Neglect friction.
Solution
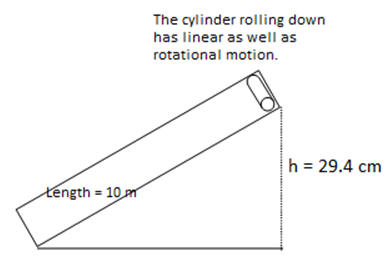
Theory: When the cylinder is at the top of the incline, it posses potential energy and when the cylinder slides down it is converted to the K.E of the cylinder. While rolling down, it has translational as well as rotational motion. So the total Kinetic energy of the cylinder is contributed by both types of motion.
Given: Diameter of the cylinder = 50 cm = 0.50 m
Radius = 0.50/2 = 0.25 m Height of the incline = 29.4 cm Length of the incline = 10 m
Required: Linear speed = v =? Angular speed = ω =?
Now the potential energy at the top of incline = mgh = 9.8 × 29.4m
K.E at the bottom = ½ mv2 (1)
Rotational energy at the bottom = ½ Iω2 (2)
For a solid cylinder, I = ½ mr2 (3)
Also, v = ωr OR ω = v/r (4)
At the end of the slide, the potential energy is converted to kinetic energy.
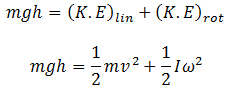
Put the value of I from equation (3) and ω from equation (4).
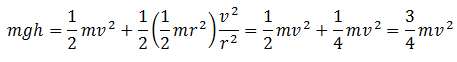
Cancelling m on both sides and putting the value of ‘g’ and ‘h’,
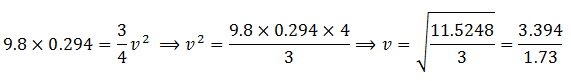
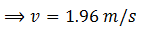
Now for angular velocity, use equation (4)
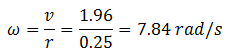

Pingback:numerical-problem on finding the velocity of a rolling disc – msa
Pingback:K.E of a rotating ball, Physics 11 – msa
Pingback:Numerical Problems on Rotatory and Circular Motion, Physics Grade 11 – msa
Pingback:numerical-problems-on-circular-and-rotatory-motion-chapter-4-physics-11