Problem 6: Calculate the speed of efflux of kerosene oil from a narrow hole of a tank in which pressure is 4 * 10^-3 atm. Density of kerosene oil is 72 kg m^-3. (one atmosphere = 1.03 * 10⁵ pa).

Answer

Given data              Pressure = 4 × 10^-3 atm = 4 × 10^-3 ×  1.03 × 10⁵ pa = 4.12 × 10² pa

                                   Density of kerosene oil =0. 72 kg/m²

Required                         Speed of efflux = v =?

Formula                           Torricelli’s Theorem

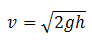
Theory: Since we are not given with the height h of the tank, so to use the above formula we first find the height of the tank. As

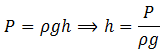
Put the values from the given data

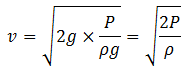
Put the values in the formula from the given data

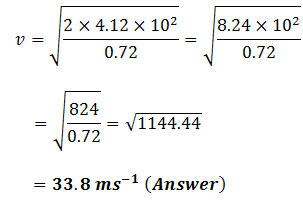
This is the required velocity of efflux.

Velocity of efflux means the average flow rate of kerosene oil emitted from the tank in the atmosphere.