Problem 7: Find the magnitude of the forces provided by the supports A and B if shown in balanced condition. Weight of plank is 500 N and it is uniform in shape. Weight of the bloc= 100 N, Weight of the student = 500 N.
Solution
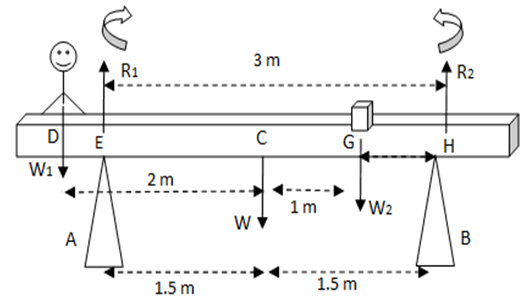
Strategy: Consider the figure. We have to find the forces due to supports A and B in order to keep the plank in a balanced condition. We apply the conditions of equilibrium, i-e,
Given data
Weights
Weight of the plank = W = 500 N
Weight of the student = W1 = 500 N
Weight of block = W2 = 100 N
Distances
DC = 2 m
EC = 1.5 m
CG = 1 m
CH = 1.5 m
Required
Force by support A = R1 =?
Force by support B = R2 =?
Now using the first condition of equilibrium
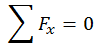
Look at the fig. No force is acting along
x-axis. Therefore,
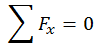
Similarly
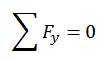
Taking the upward forces as positive and the
downward as negative,
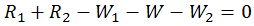
Put the values
R1 + R2 – 500 – 500 – 100 = 0
R1 + R2 = 1100
OR R1 = 1100 – R2 —–
(A)
Now apply the 2nd condition of
equilibrium
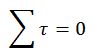
Let the body rotates about point C and the
anti-clockwise torques as positive
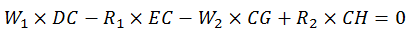
Put the values
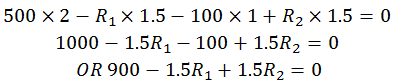
Put the value from equation (A)
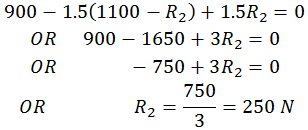
Put this value in equation (A)
R1 = 1100 – 250 = 850 N
So the reaction force on the
plank provided by the supports at points A and B are 850 N and 250 N
respectively.

Pingback:numerical-problem-8-chapter-2-physics-11 – msa
Pingback:numerical-problem-6-chapter-2-physics-11 – msa
Pingback:Numerical on Vectors and Equilibrium, Physics 11 – msa