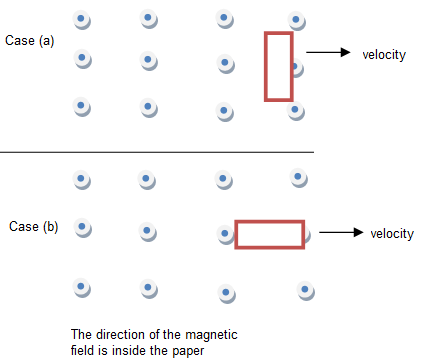
Problem 8: A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the cut if the velocity of the loop is 1 cms-1 in a direction normal to (a) longer side (b) shorter side of the loop? For how long does the induced voltage lasts in each case?
Solution
Given Length of the loop, l = 8 cm = 8 × 10-2 m, Breadth of the loop, b = 2 cm = 2 × 10-2 cm
Strength of uniform magnetic field, B = 0.3 T, Velocity of the loop = 1 cm/s = .01 m/s
Asked ϵ when (a) v normal to l, (b) v is normal to b
Formulae (i) When the loop is moved in the magnetic field, work is done on it which converts to electrical energy and a motional emf is produced given by, ϵ = Blv,
(ii) s = vt
- Apply formula (i) to find the induced emf, for longer side normal to v.
ϵ = 0.3 × 8 × 10-2 × 10-2 = 2.4 × 10-4 V
- Using the same formula when the shorter side is perpendicular to v.
ϵ =.3 × 2 × 10-2× 1× 10-2 = 0.6×10-4 V
Time for which the induced voltage will last is the time the loop takes to move out of the field. So we apply formula (ii) to find t.
In the first case,
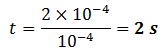
In the second case,
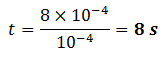

Pingback:numerical-problem-9-electromagnetic-induction-physics-12-msa – msa
Pingback:numerical-problem-7-electromagnetic-induction-physics-12 – msa
Pingback:numerical-problems-on-electromagnetic-induction-chapter-4-physics-12