Problem 8: Compute the following to correct significant digits:

Solution

(a) 3.85 m × 3.9 m

Hint: see question 4 in comprehensive questions, rule for indicating uncertainty in product.

Now 3.85 m × 3.9 m = 15.015 m²

We know that in case of multiplication, the number of sig figs in the final result is equal to the least number of sig figs in the measurement of the numbers to be multiplied. Here, the number of sig figs in 3.85 is three and the number of sig figs in 3.9 is two. So to compute the product to correct significant digits, we round off the final result 15.015 to 2 sig figs. Therefore,

3.85 × 3.9 = 15.015 m² = 15 m²

(b) 1023 kg + 8.5489 kg

Now 1023 kg + 8.5489 kg = 1031.5489 kg.

Rule: In case of addition (and also subtraction) the final result is determined by the greater uncertainty (or less precision). In the given numbers, 1023 is less precise (has greater uncertainty) than 8.5489. Number of significant figures in 1023 is 4. Therefore, the final result would have 4 sig figs.

Now 1023 + 8.5489 = 1031.5489 kg = 1032 kg. (Result limited to 4 sig figs with the use rule for rounding off).

(c) 22/7 = 3.14285714…….

Rule: In case of division the final result is limited to the number with least number of sig figs.

The number has an infinite number of sig figs. Looking at the nature of 22/7, the final result can be rounded off to one sig fig (the number of sig figs in the denominator). Therefore,

22/7 = 3

(d)

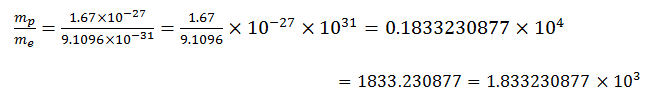
Now the number of sig figs in the measurement of numerator is 3 and the denominator is 5. Therefore, according to rule, we have to round off the final result to 3 significant figures. Therefore,

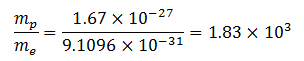
This is the required result.