Problem 9: A rectangular metallic piece is (3.7 0.01) cm wide, and (7.20 0.01) cm long.
(a) Find the area of the rectangular metallic piece and uncertainty in the area.
(b) Verify that the sum of the percentage uncertainty in the length and in the width is equal to 0.4%.
Solution
(a) Given data: width of the rectangular metallic piece = (3.7 ± 0.01) cm
Length of the rectangular metallic piece = (7.20 ± 0.01) cm
Required: Area of the piece =?
Uncertainty in the area =?
Strategy: First we find the percentage uncertainty in the length and width. The product rule for finding the percentage uncertainty in the final result is both the percentage uncertainties are added. From this percentage uncertainty in the final result we calculate the uncertainty in the actual value of the product (= area of the rectangular piece).
Now
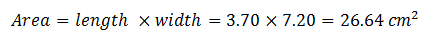
In the product, the number with least sig figs is 3 (in fact 3 in both numbers), therefore, the area is rounded off to 3 significant figures. Therefore, Area = 26.6 cm2 —— (A)
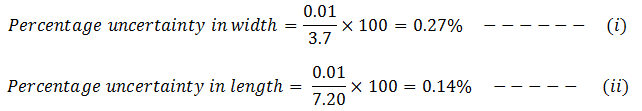
Using the product rule to find the percentage uncertainty in the area,
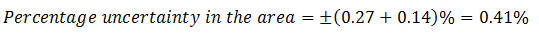
This is uncertainty in 100 cm2 of the area. We need to find uncertainty in 26.6 cm2 (equation A), which is the actual area of the metallic piece.
Hence uncertainty in 26.6 is
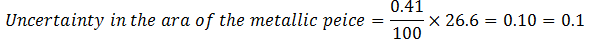
Therefore,
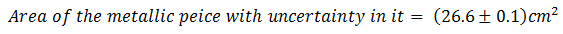
This was required.
(b) Given data: width of the rectangular metallic piece = (3.7 ± 0.01) cm
Length of the rectangular metallic piece = (7.20 ± 0.01) cm
Required: Find sum of the percentage uncertainty in the length and in the width
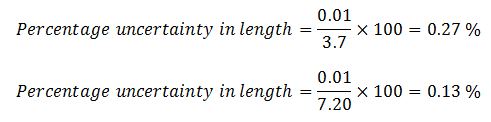
Therefore, sum of the percentage uncertainties in width and length = 0.27% + 0.13% = 4 %
Hence proved.

Pingback:numerical-problems-on-measurement-physics-11