Problem 9: A resistor of 30 ohm is connected in series with a capacitor of 79.5 μF across a power supply of 50 Hz and 100 V. Find (a) impedance (b) current (c) phase angle and (d) equation of instantaneous current.Add Your Heading Text Here
Solution
Given
Capacitance, C = 79.5 μF = 79.5 × 10-6 F
Resistance, R = 30 Ω
Supply frequency, f = 50 Hz
Supply voltage, V = 100 V
Find: Z, I, ϕ, Iinst
(a) Equation for the impedance of a capacitive circuit is,
Now, 
Put the values,
Therefore,
(b) Current in the circuit is determined by Ohm’s law,
(c) Phase angle ϕ is given by,
Put the values,
(d) Instantaneous current in a capacitive circuit is given by,
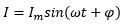
Which means the current leads the voltage by phase angle ϕ. Im is not given, therefore, we calculate it from the formula, Im = Irms/0.707. Put the value of effective current calculated in (b), we have, Im = 2/0.707 = 2.828 A. Similarly, ω = 2πf. Put the value of frequency, ω = 2× 3.14× 50 = 314 rad/s. Put all these values in the above equation, we have
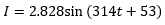
This is the required equation.
Pingback:Numerical Problem 10, AC Circuit, Physics 12 … msa – msa
Pingback:Numerical Problem 8, Alternating Current Circuit, Physics 12 … msa – msa
Pingback:solved-numerical-problems-alternating-current-circuit-physics-12-msa – msa