Question 7: Define torque. Show that torque is the vector product of force and position vector.
Answer
Definition of torque or moment of force
Turning effect produced in a body about a fixed point due to applied force is called torque or moment of force.
Torque produces angular acceleration like force which produces linear acceleration. The turning effect depends upon the moment arm r, the applied force F and angle θ between them. Mathematically,
Where θ is the angle between r and F and n̂ is a unit vector perpendicular to the plane of r and F. Thus, torque is a vector quantity. Its unit is N.m.
Explanation of torque or moment of force
See the fig below.
A rod is rotated about an axis. The force F causing rotation acts at a point near the opposite end. The distance between the axis and the point of action of force is called position vector, r.
Resolve F into rectangular components along the position vector, r. Component Fcosθ acts through the axis, along the position vector r and therefore, produces no torque. Component of force, Fsinθ acts perpendicular to the position vector r and causes the entire torque in the rod.
The above equation for torque can be written as
and we can equally define torque as “its magnitude is the product of position vector r and the component of force acting perpendicular to it”.
Now consider this diagram.
‘d’ is the shortest distance = rsinθ, from the axis of rotation to the line of action of force. The torque equation can be written as
Therefore, the magnitude of the torque can also be said to be dF “product of applied force and the shortest distance between the axis point (pivot) and line of action of force”.
In many cases, this approach to the calculation of magnitude of the torque is easier than that of resolving the force into components and multiplying its perpendicular component with position vector r and therefore followed.
Factors on which torque depends
Looking into the equation for the calculation of torque, it is easy to understand that the torque depends on the following factors.
- Force, F: Greater the magnitude of F, greater will be the torque produced if r and θ is constant.
- Position vector, r: Longer the position vector, greater the torque produced and vice versa.
- Angle of force and position vector, θ: Torque will be maximum if the angle θ between r and F is 90° or 270°. Similarly, torque is zero if the angle is 0° or 180°.
WHY TORQUE = FORCE × MOMENT ARM?
As already stated, torque depends upon the applied force and moment arm. This is quite clear that an increased force will produce more turning effect or torque and if the force is decreased the turning effect will also decrease. In the same way, increasing the moment arm will also increase the torque and vice versa.
An interesting situation arises with changing the direction of the force. When we gradually change the direction of the force, the torque is also gradually changed. Few situations are hereby depicted in the adjacent fig.
- Force F is acting on a rod rotating around the pivot ‘O’. F is making an angle θ = 0° with r . The line of action of force passes through the center of pivot in this case. No turning effect is produced.
- Now let the direction of force is changed. It acts at an angle 90° with r. It is our common experience that the turning effect is now maximum.
- Let the direction of force is further changed. Now the force is making an angle of 180° with the moment arm . We observe the torque is again zero.
To analyze the results of our experiment, we know that sin0° = 0. And when the angle between r and F is zero, the torque is also zero.
The torque is maximum at angle 90°. Sinθ value is also maximum at this angle.
Torque is again 0 when the angle is 180°. Sine value of the 180° is also zero.
The conclusion is the turning effect or torque is proportional to the sine value of the angle between r and F. Therefore, torque is proportional to the magnitude of the force applied, magnitude of moment arm and the sine of the angle between them. Therefore,
= rFsinθ
This is exactly what the vector product is. Therefore,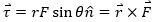 
Thus, torque is equal to the vector product of force and moment arm.
Pingback:Comprehensive Questions, Vectors and Equilibrium … msa