Question 4: Prove that absolute ![]() .
.
Answer
Absolute potential energy of a body at the surface of earth is equal to the work done in lifting the body from the surface of earth to the infinity. The infinity point is one where the force due to gravity is negligible or non-existent.
Hence for absolute potential energy we have to fix a zero point for the potential energy. The zero point is so far away the earth that it is no more affected from the attraction of the earth.
While deriving the expression for the PE over height ‘h’ we have got that P.E = mgh . Here we assume that the weight of the body (= mg) remains constant. But this assumption does not hold when we deal with great distances over the surface of earth. Therefore, the scheme of mathematical calculation is we find the work done between two points 1 and ‘N’. The distance between 1 and ‘N’ is divided into small elements of distances such that the value of ‘g’ remains constant over each element of distance. Put point 1 at the surface of earth as shown in the figure.
Now consider a body of mass ‘m’ at point 1 as shown in the figure. Let the respective distances of points 1,2,3, ………, N from the center of the earth are, r1, r2, r3, ……….. rN.
Work done from point 1 to point 2 is,
![]()
Where the average force is ![]()
Therefore,
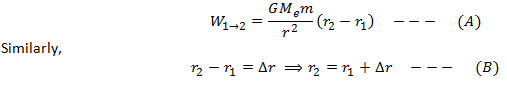
Suppose ‘r’ is the average distances of point 1 and point 2 from the earth. From the figure,
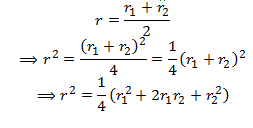
Put the value of r2 from (B),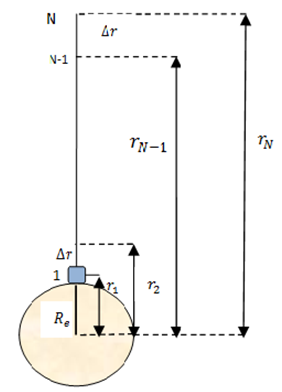
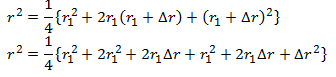
Simplifying,
![]()
As Δr is very small, its square can be neglected.
![]()
Substitute the value of Δr,
![]()
Put this value in equation (A)
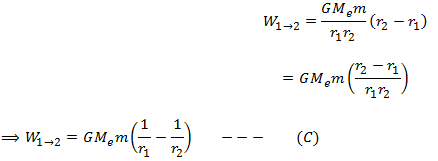
Similarly
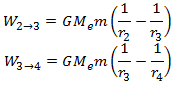
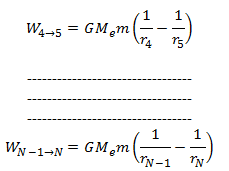
Now the work done from 1 to N will be the sum of all these incremental works.
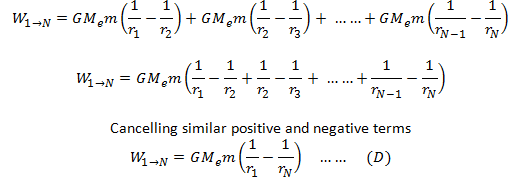
Now to find the absolute potential energy, point N must be on infinity. Put rN = ∞, we have,
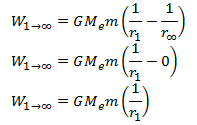
If the body is at the surface of the earth, r1 = Re = Radius of the earth.
So if we put this value of r1 in the above equation, we will get the work done in moving the body from the earth surface to infinity and, by definition, will be equal to the absolute potential energy of the body. Therefore,
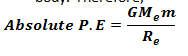
Hence proved.

Pingback:Work, Power and Energy, Comprehensive Questions – msa