Question 2: For a simple motor, why must the back emf always be smaller than the applied potential difference?
ANSWER
We know in an electric motor, current is supplied to a coil placed in a magnetic field. When the current starts to flow in the coil, a magnetic field is produced around it. Now this magnetic field interacts with the external magnetic field resulting in a force on the coil. The force rotates the coil. The rotating coil in the external magnetic fields now links (that is connects to) a changing magnetic flux (Remember when the angle between the coil and constant magnetic field changes, the number of magnetic lines of force passing through the coil also change). By Faraday’s law, an emf is induced in the coil. By Lenz’s law, this induced emf opposes the applied emf, i-e, its polarity is opposite to the applied voltage. When the applied emf (applied voltage) is opposed by the induced emf (which is also a voltage), it decreases the effective voltage across the conductor. If V is the applied voltage, R is the resistance in the coil, I is the current flowing and ϵ is the back emf, then
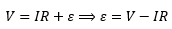
This equation indicates the back emf will always be less than the applied voltage by an amount IR.
Now let’s see what actually happens.
When we start the motor by switching it on, maximum current goes into the coil. However, due to the interaction of both magnetic fields (as stated above) the coil starts rotating. With the rotation of coil a back emf is induced. As the coil gets speed, the back emf also increases. The difference between the applied voltage and back emf decreases.
Applying Ohm’s law, the current I in the coil is
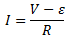
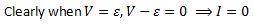
When the current decreases, the angular speed of the coil also decreases which in turn decreases the back emf. Therefore, back emf ϵ can never exceed the applied voltage. (Remember applied voltage is constant).

if velocity of coil decrease then back emf decrease which res
ults in more current throughout the motor….but not decrease the current.
Pingback:factors-limiting-back-emf – msa
Pingback:similarities-and-differences-in-motor-effect-and-electromagnetic-induction – msa
Pingback:sq-ch4-p12 – msa