Question 1: Define work and show that it is the dot product of force and displacement. At what conditions work done will be maximum or minimum?
Answer
Work
Work has a specific definition in physics. Work is done when a force is exerted on an object, and the object moves from one place to another. So work is said to be the result of the force, acting over a certain distance. This distance is called the displacement of the object. If the force F, and the displacement d, are in the same direction, then the work W is given by the formula,
W = Fd
The work is the product of the force and the displacement. In SI (international system) units, the unit of force is the newton (N), and the unit of distance or displacement is the meter (m). Therefore, the unit of work can be expressed as a newton-meter, N∙m. This much amount of work is also known as a Joule, J. The newton is a compound unit, and so a Joule is also equal to,
![]()
The equation W = Fd depends on the force and the displacement being in the same direction. There are many situations in which their directions are different, for example, a person pushing on a box close to the ground. A component of the force the person applies is directed down, even though the resulting direction of the box is forward. In a case like this, only the component of the force that is along the path of the box’s displacement contributes to the work done.
Similarly, if we treat the force and the displacement as vectors, the work can be found by using the dot product (also known as the scalar product). The work is equal to,
Work = ![]() .
.![]()
Or Work = W = Fd cosθ
In this formula, θ is the angle between the force and displacement vectors, and F and d are the magnitudes of the vectors.
Work as dot product of ![]() and
and ![]()
Suppose ![]() is the applied force on a body and
is the applied force on a body and ![]() is the resultant displacement. Let the angle between
is the resultant displacement. Let the angle between ![]() and
and ![]() is θ as shown in the figure.
is θ as shown in the figure.
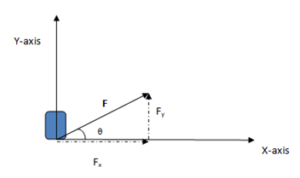
In this case, force and displacement are not in the same direction. However, if we resolve ![]() into its rectangular components, then
into its rectangular components, then ![]() is the component of force along the displacement. This is in fact the effective component of the force which causes displacement. Therefore,
is the component of force along the displacement. This is in fact the effective component of the force which causes displacement. Therefore,
Work = F.d
W = Fcosθd = Fdcosθ
If we decrease the angle θ, its cosine value will increase. Consequently more work will be done.
On the other hand if we increase the angle between ![]() and
and ![]() , the cosine value of θ will decrease. The work done will also decrease when we change the direction of force upward. So, it is concluded that,
, the cosine value of θ will decrease. The work done will also decrease when we change the direction of force upward. So, it is concluded that,
Work = Fdcosθ
But Fdcosθ =![]() .
.![]()
Therefore, we can say that work is the dot product of ![]() and
and ![]() .
.
Maximum Work
From the above equation it is clear that work depends upon,
- Force : Greater the force, greater will be the work done, provided displacement
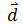 and angle θ are constant.
and angle θ are constant. - Displacement : Greater the displacement, greater will be the work done, provided
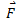 and θ are constant.
and θ are constant. - Angle θ: Greater the value of cosθ, greater will be the work done, provided
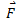 and
and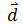 are constant.
are constant.
Maximum Work
For maximum work by a constant force ![]() , however, cosθ should be maximum when
, however, cosθ should be maximum when ![]() and
and ![]() happen to be constant. This means θ = 0°.
happen to be constant. This means θ = 0°.
So, for maximum work to be done by a force ![]() , then
, then ![]() and
and![]() must be in the same direction, i-e, θ = 0°.
must be in the same direction, i-e, θ = 0°.
Minimum Work
For a constant force ![]() , work will be minimum if the value of cosθ is minimum. The cos value of θ is minimum when θ = 180°.
, work will be minimum if the value of cosθ is minimum. The cos value of θ is minimum when θ = 180°.
Thus for minimum work, ![]() and
and ![]() must be in opposite directions.
must be in opposite directions.

Pingback:Work, Power and Energy, Comprehensive Questions – msa