Quantitative nature of K.E

Question 4: Is kinetic energy a vector quantity?

ANSWER

No, Kinetic energy is not a vector quantity. Like any other form of energies, Kinetic Energy is also a scalar quantity. If ‘m’ is the mass of a body and ‘v’ is the speed with which it is moving (magnitude of velocity), its kinetic energy is given by,

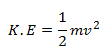
Here v² is calculated as the dot product of the velocity vector with itself. Therefore, from mathematics point of view, it is the product of two scalar quantities, m and v², and must be a scalar.

Physically, it has only magnitude and no direction. An interesting angle to see the problem through is, it is the work done on a body which appears as K.E. As work is a scalar quantity, so is K.E.

Therefore, the quantitative nature of K.E is scalar.

Why v² = v.v and not v × v?
There might be two arguments that v2 = v.v and not v × v?
As a rule of thumb, we look at the value of the product we get. If it needs a direction for its specification, it is a vector product, otherwise a scalar. Now, the same quantity of fuel energy can take a car to east or west or even in a circle. Therefore, we conclude kinetic energy is also a scalar as the fuel energy.

– Second, the angle between v and v is zero and hence v × v must be zero as sin0° = 0. But we see the K.E of a body is not zero as the moving body has the ability to do work. Therefore, it must be a dot product.

4 Comments

Leave a Reply Cancel reply