Show that in angular form, centripetal acceleration is:

ANSWER

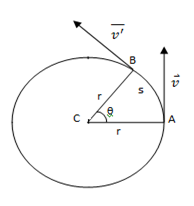Consider a body moving in a circular path. Let at any instant of time t₁ it is at a point A on the circumference of the circle. Suppose it moves with a velocity  and at time t₂, it is positioned at point B on the circle. The motion is an accelerated one due to its changing direction and let’s further suppose its velocity to be  at B. Let the change in time is  Δt = t₂-t₁ and change in velocity is  . If Δt is very small, point B and point A will be very close to one another and we can say,

S = vΔt

Similarly, we know that

(See question 1, centripetal acceleration).

So, substituting for the value of ‘S’, in the above equation, we got 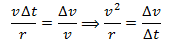Since 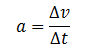, therefore . Considering in vector form, 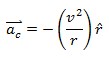                                                                                                             …       (1) The negative sign is used because the centripetal acceleration is directed towards the center of the circle whereas radius of the circle is directed outward. Therefore, both   and   are opposite in direction to one another. In addition, we know that,

v = rω       …      (2)

So to substitute for v in equation (1) 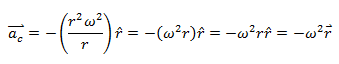This proves the result.