Question 1: What are the centripetal acceleration and centripetal force? Derive their equations.

ANSWER

We know that when no unbalanced force is acting on a moving body, it will continue to move in a straight line with uniform velocity. A body moving in a circle or curve, therefore, is experiencing some force compelling it to move in that path.

Centripetal Force

The force, which compels a body to move in a circular path, is called centripetal (or center-seeking) force.

Mathematically,

                                                                                                           …           (1)

Centripetal Acceleration

The change in the direction of the velocity of the body produces acceleration that is directed to the center of the circle, called centripetal (or center-seeking) acceleration, denoted by .

Mathematically,

                                                                                                      …              (2)

Equation for centripetal acceleration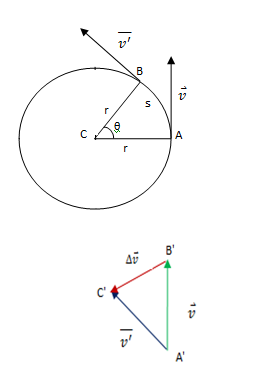

Consider a body of mass m is moving with uniform velocity v in a circle of radius r and center at C. At point ‘A’ at time t₁, velocity of the body is  . Then at point ‘B’ when time is t₂, its velocity changes to  .  Now let us construct a triangle A’B’C’ so that A’B’ is equal and parallel to   and A’C’ is equal and parallel to .  As the speed does not change, the velocity has the same magnitude with a changed direction. The change in velocity is  in a time interval Δt = t₂– t₁.

When Δt is very small, Δ  is also very small and the arc is approximately equal to cord AB. Then on comparison, ΔACB and ΔA’B’C’ are isosceles. So,

If Δt is very small, and hence do θ, point B is very close to point A, then,

S = rΔt

Use this value of ’s’ in the above equation.

The RHS is the instantaneous acceleration. Thus

This is the required equation of centripetal acceleration.
In vector form,

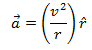
Here   is the centripetal acceleration.
 is the unit vector along the radius acting outward from the center of the circle.

Both the centripetal acceleration and the radius vector are, therefore, opposite in direction with each other. Therefore, we have,

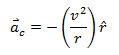
This is the equation of centripetal acceleration.

Equation for centripetal force

From Newton’s Second Law of Motion, F = ma

Putting the value of acceleration, we get,

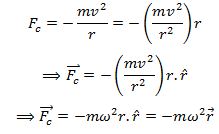
This is the required equation for the centripetal force.