Question 6: State Ampere’s Law and use it to derive an expression for the magnetic field of a solenoid.
ANSWER
Statement of Ampere’s law
The sum of the dot products B.L around a closed path in the magnetic field B of a current is equal to μ0 times the current I crossing the surface enclosed by the path.
Mathematically,
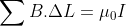
Consider a long straight current carrying wire. By experiments and cylindrical symmetry of the wire, it is obvious that;

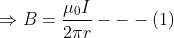
Where 0/2π is the constant of proportionality and μ = 4π×10-7 is the permeability of the free space.
Consider the figure where a current I is passing through a long wire and we take a circle of radius r around it. Let’s go around the circle and calculate B.L. Divide the circular path into very large number of small elements each of length ΔL. Since the lines of B are circular, ΔL is parallel to B along each small element.
B.ΔL = BΔL

This is Ampere’s circuital law. The closed path is called Amperian path.
Experiments show this law is valid for any steady magnetic field, any assembly of currents and any closed path.
Magnetic Field due to a solenoid
A solenoid is a fine wire wound in the form of a helix around a cylindrical surface.
When current is passed through the wire of a solenoid it behaves like a magnet of the same shape. Suppose a current I is flowing through a long solenoid as shown in the fig. The resulting field from the current I is stronger and uniform inside the solenoid and weaker outside the solenoid.

The magnetic field B is along the axis of the solenoid and its direction is determined by the RHR, which states, “hold the solenoid in your right hand with fingers curling in the direction of the (conventional) current, the thumb will point in the direction of the ield.”
Let’s calculate B within the solenoid. We consider an Amperian path (closed path) abcd as shown below. Applying Amperian’s Circuital law,



Now, inside solenoid, B is parallel to l1 and hence B.l1 = Bl1cos00 = Bl1
Outside solenoid, B is zero, therefore, B.l3 = 0. B is perpendicular to l2 and l4, therefore, B.l2 = B.l4 = 0. So adding all B.ls along the amperian path,

Hence Bl1 = μ0I.
Now if there are n turns of the solenoid per unit length, then nl1 current elements with current I each enclosed in the amperian path. So we have,

This is the expression for the magnetic field due to a current-carrying solenoid.

Pingback:Galvanometer, its conversion to an ammeter and voltmeter … msa – msa
Pingback:what-is-magnetic-flux – msa
Pingback:1924