Question 6: Describe the construction of a capacitor and derive an equation for the energy stored in a capacitor.
The capability of a capacitor of storing charge is called its capacitance.
The charge Q which resides on one of these plates depends upon the potential difference between them. The large the voltage of the battery (which provides the potential difference between the plates), the greater will be the charge on the capacitor.
Q ∝ V or Q = CV
Where C = Q/V is the constant of proportionality called the capacitance of the capacitor. It depends upon the geometry of the capacitor. From the above equation, it is defined as the capacitance C of a capacitor is the ratio of the magnitude of charge on either plate to the potential difference between the plates.
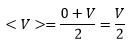Now the electrical potential energy is given by
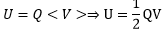As Q =CV, therefore,
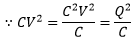Therefore, we can write,
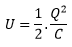
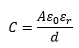for parallel plates capacitor. Substituting the values in equation (1)
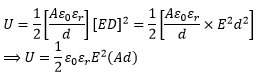Since A is the area of each plate and d is their separation, Ad = volume enclosed by the capacitor.
Now if u is the energy density (energy per unit volume), then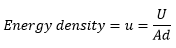
Put the value of U.
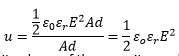This equation gives the energy per unit volume of the capacitor and valid for any electric field strength.
ANSWER
Capacitor
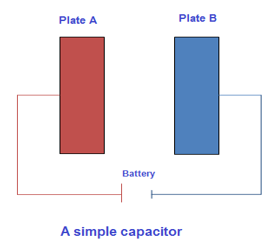
A device used for storing electric charge is called a capacitor. It is also known as condenser.Construction
The simplest capacitor consists of two parallel metal plates having equal but opposite charges and separated by a small distance. The plates have same size and shape. The space between the plates is filled with some insulator such as air, paper, mica etc. Charge is transferred from one plate to another by means of a battery. Charge lost by one plate is equal to the charge gained by the other plate; hence the charge on one plate is +Q and that on the other is -Q. The charge remains on the inner surfaces of the plates. A typical capacitor can store a large amount of charge (and hence energy) in a small space.
The capability of a capacitor of storing charge is called its capacitance.
The charge Q which resides on one of these plates depends upon the potential difference between them. The large the voltage of the battery (which provides the potential difference between the plates), the greater will be the charge on the capacitor.
Q ∝ V or Q = CV
Where C = Q/V is the constant of proportionality called the capacitance of the capacitor. It depends upon the geometry of the capacitor. From the above equation, it is defined as the capacitance C of a capacitor is the ratio of the magnitude of charge on either plate to the potential difference between the plates.
Unit
SI unit of charge is coulomb and that of potential difference is volt. Therefore, the unit of capacitance C (= Q/V) is coulomb per volt. This unit is called farad (after famous British Scientist Michael Faraday). It is defined as the capacity of that capacitor which stores a charge of 1 coulomb having the potential difference of 1 volt between the plates. Farad is a big unit and for practical purposes its submultiples, micro farad = 10-6 farad and Pico farad =10-12 farad are used.Energy stored in a capacitor
A capacitor is a device to store the charge thereby storing electrical energy. Work is to be done to deposit charge on the plates of the capacitor, therefore, if the capacitor is initially uncharged, the potential difference between the plates is zero. When they are connected to the opposite terminals of the battery, charges +Q and -Q deposit on the respective plates. After some time, the potential difference between the plates becomes V, the voltage of the applied battery. Thus the average potential difference between the plates is,
Now the electrical potential energy is given by
As Q =CV, therefore,
Therefore, we can write,
Electric field and the energy stored
When we consider electric field between the plates, it is even more useful to consider that the energy is stored in the field between the plates. In such a case we know that V = Ed and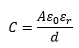
for parallel plates capacitor. Substituting the values in equation (1)
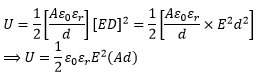Since A is the area of each plate and d is their separation, Ad = volume enclosed by the capacitor.
Now if u is the energy density (energy per unit volume), then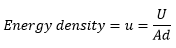
Put the value of U.
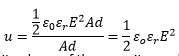This equation gives the energy per unit volume of the capacitor and valid for any electric field strength.
Pingback:Electrostatics, Physics 12 … msas – msa
Pingback:equi-potential-surfaces and lines … msa – msa
Pingback:electric-potential-and-derivation-of-formula-for-electric-potential – msa