Question 7: Describe the concept of equipotential surfaces and derive an expression for electric field as negative of potential gradient.
ANSWER

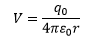
Since (q0/4πε0) is constant for a particular charge, therefore, electric potential depends upon the distance from the point charge. So at all equidistant points the potential would have same value. Since electric field due to a point charge extends in all directions (three dimensions) therefore, the equipotential surfaces are in the form of concentric spheres with the point charge at the center. However, if we deal with a two-dimensional case, concentric circular lines around the point charge make equipotential lines. Equipotential surfaces/lines have some important characteristics: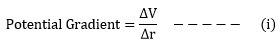 Potential gradient is used to find the magnitude and direction of electric intensity.
Potential gradient is used to find the magnitude and direction of electric intensity.
Consider a positive test charge q0 in an electric field. The electric force on the charge is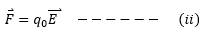 Let an opposite force is applied on the charge in the state of equilibrium to move it from point A to point B. Let the work done on the charge is WAB. The potential difference (work done per unit charge) is given by
Let an opposite force is applied on the charge in the state of equilibrium to move it from point A to point B. Let the work done on the charge is WAB. The potential difference (work done per unit charge) is given by
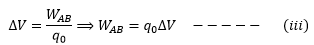 Also
Also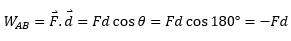 Put the value of F from equation (ii).
Put the value of F from equation (ii).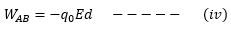 Compare (iii) and (iv)
Compare (iii) and (iv)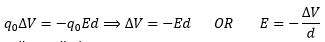 If we put d = Δr; infinitesimally small, then
If we put d = Δr; infinitesimally small, then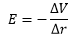 As Δr is very very small and hence a perpendicular distance (straight line), ΔV/Δr gives the maximum value of the rate of change of potential with displacement. Therefore, the electric field intensity is the negative of the gradient of potential.
As Δr is very very small and hence a perpendicular distance (straight line), ΔV/Δr gives the maximum value of the rate of change of potential with displacement. Therefore, the electric field intensity is the negative of the gradient of potential.
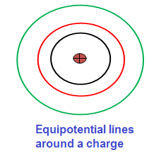
Equipotential surfaces/lines
An equipotential surface (or line) connects all those points in space where the potential due to an electric field is same. For a point charge
Since (q0/4πε0) is constant for a particular charge, therefore, electric potential depends upon the distance from the point charge. So at all equidistant points the potential would have same value. Since electric field due to a point charge extends in all directions (three dimensions) therefore, the equipotential surfaces are in the form of concentric spheres with the point charge at the center. However, if we deal with a two-dimensional case, concentric circular lines around the point charge make equipotential lines. Equipotential surfaces/lines have some important characteristics:
- No two surfaces cross each other.
- No work is done in moving a charge from one point to another on the equipotential surfaces or lines.
- Electric potential is a scalar quantity. However, potential may be positive or negative depending upon on the sign of charge producing it.
- If there are two or more charges, the electric potential at a particular point is the scalar sum of potentials due to individual charges.
- If the electric field is stronger, the lines on the equipotential surface would be close together. So the electric potential energy which is inversely proportional to r is changing by a large amount in small distances and there must be a large force acting.
Potential gradient
The rate of change of potential ΔV with respect to displacement Δr is called potential gradient.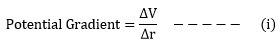 Potential gradient is used to find the magnitude and direction of electric intensity.
Potential gradient is used to find the magnitude and direction of electric intensity.Consider a positive test charge q0 in an electric field. The electric force on the charge is


Pingback:electric-polarization-and-capacitance – msa
Pingback:capacitor-and-its-energy – msa
Pingback:index-ch11-p12