Question 5: Explain the concept of electric potential. Derive expression for electric potential at a field point due to a source.
ANSWER
Concept of electric potential
A point charge has a spherical region around it where any other charge experiences an attractive or repulsive force, depending upon the nature of the two charges. This force is inversely proportional to the square of the distance between the two charges. This region is called the electric field. In a way, it is similar to the earth gravitational field.
So the force varies rapidly as we go away or come near to the charge. When we move a certain charge against the electric field intensity, we have to do some work on the charge. This work stores in the charge as its potential energy. When released the potential energy stored converts to the kinetic energy of the charge and it accelerates back toward its previous position.
Definition of Electric Potential
Electric Potential is defined as the work done in bringing a unit positive charge from infinity to a certain point against the electric field intensity keeping the electric equilibrium.
Expression for electric potential
Consider an isolated charge +Q in space. If a positive field test charge q is placed at infinity, it will not experience any force. However, if the charge is slowly moved toward +Q it will experience a force of repulsion. As this force is inversely proportional to the square of the distance between them, it increases as the distance decreases. So work is to be done if it is brought to point A.
Now electric field doesn’t remain constant due to inverse proportionality to r2.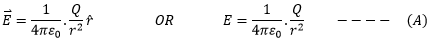
So to keep ![]() constant, we divide ‘r’ into very very small intervals Δr, so that
constant, we divide ‘r’ into very very small intervals Δr, so that![]() is practically constant over this interval. Now that F = qE and work done = F.d.
is practically constant over this interval. Now that F = qE and work done = F.d.
Put the value of E from equation (A)![]()
Now to calculate the work done in bringing the charge q from point A at distance rA from the source charge to point B at distance rB from the source charge. The distance is quite large; therefore, we divide it into small distances of Δr each over which![]() can be taken constant. To calculate the work done between the first interval from rA to r1, note that:
can be taken constant. To calculate the work done between the first interval from rA to r1, note that:
Square of the average of the two distances is![]()
(This can be proved mathematically.)
![]()
Put these values in equation (B)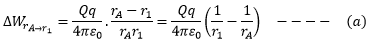
Similarly, for the second small interval, Δr = r1 – r2 and the work done is
![]()
In the same way
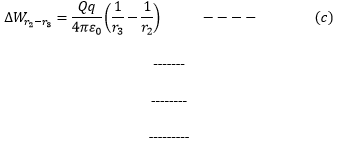
Similarly to point B at distance rB,
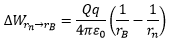
Total work done in moving the charge from point A to point B is the sum of all works over all small intervals Δr. Adding them all,
![]()
Cancelling opposite terms.
![]()
Let A is at infinity, then the work done in moving a test charge from infinity to a distance r from Q is,
![]()
This is the amount of work done in bringing charge q from infinity to point B and is stored as electric potential energy in the charge. Generally, the potential energy at a distance r from Q is,![]()
Electric potential is the PE per unit charge; dividing by q,
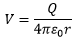
The above equation gives the potential at a certain point, distant r, due to charge Q.

Please solve all physics assignments of text book
Anwar
Okay. Soon, IA.
Pingback:capacitor-and-its-energy – msa
Pingback:Electrostatics, Physics 12 … msas – msa
Pingback:gauss-law-and-its-applications – msa