Question 6: Define elastic and inelastic collisions. Give examples in each case. Derive mathematical equations for calculating the final velocities of the elastically colliding bodies in one dimension.
Answer
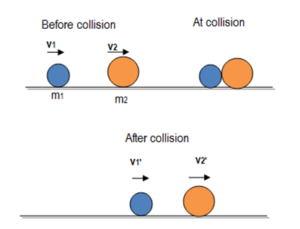 Let two balls of masses m1 and m2, respectively, collide head-on as shown in the figure. Let’s further assume m1 is approaching towards m2. Let v1 and v2 are their velocities before collision and the final velocities after collision are v1‘and v2‘ respectively. The law of conservation of momentum says that
Let two balls of masses m1 and m2, respectively, collide head-on as shown in the figure. Let’s further assume m1 is approaching towards m2. Let v1 and v2 are their velocities before collision and the final velocities after collision are v1‘and v2‘ respectively. The law of conservation of momentum says that
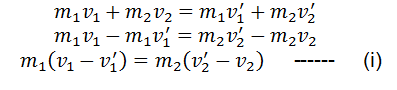 And according to law of conservation of K.E
And according to law of conservation of K.E
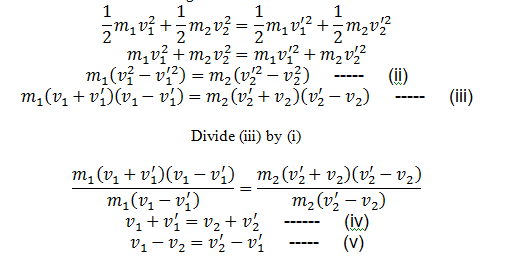 So, in case of elastic collision, the relative speed of approach (v1-v2) before collision is equal to the relative speed of separation (v2‘ – v1‘) after collision.
Final velocities of the bodies can now be calculated from the above equations.
From equation (IV)
So, in case of elastic collision, the relative speed of approach (v1-v2) before collision is equal to the relative speed of separation (v2‘ – v1‘) after collision.
Final velocities of the bodies can now be calculated from the above equations.
From equation (IV)
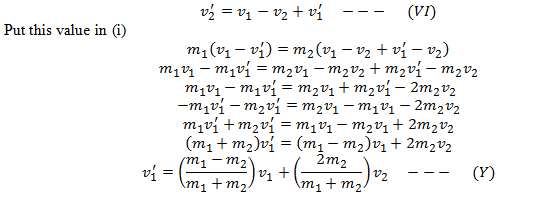 So particle ‘m1’ will go with this velocity after collision.
To find the velocity of ‘m2’ after collision, we consider equation (IV) once more.
So particle ‘m1’ will go with this velocity after collision.
To find the velocity of ‘m2’ after collision, we consider equation (IV) once more.
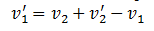 Put this value in equation (i)
Put this value in equation (i)
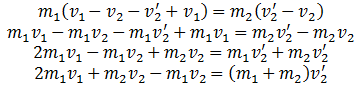
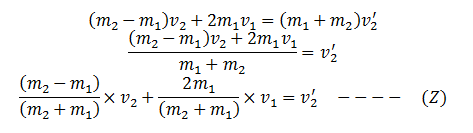 This equation represents the velocity of body m2 after collision.
This equation represents the velocity of body m2 after collision.
Elastic Collision
An elastic collision is one in which both momentum and kinetic energy is conserved. Air molecules contained in a container suffer elastic collisions with the walls of the container as an example.Inelastic Collision
An inelastic collision is one in which momentum is conserved but kinetic energy is not. In a car crash, for example, the kinetic energy is not conserved and is an example of inelastic collision. Similarly, when two lumps of clay (LOOTI) collide with one another, the collision might be one close to an inelastic one.Final velocities in elastic collision in one dimension
If before and after the collision, the motion of colliding bodies appears on a single line, the collision is said to be in one dimension or head-on. Let two balls of masses m1 and m2, respectively, collide head-on as shown in the figure. Let’s further assume m1 is approaching towards m2. Let v1 and v2 are their velocities before collision and the final velocities after collision are v1‘and v2‘ respectively. The law of conservation of momentum says that
Let two balls of masses m1 and m2, respectively, collide head-on as shown in the figure. Let’s further assume m1 is approaching towards m2. Let v1 and v2 are their velocities before collision and the final velocities after collision are v1‘and v2‘ respectively. The law of conservation of momentum says that
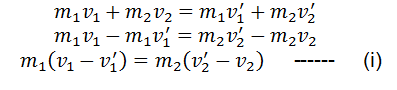 And according to law of conservation of K.E
And according to law of conservation of K.E
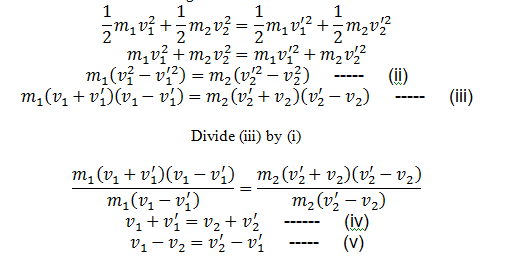 So, in case of elastic collision, the relative speed of approach (v1-v2) before collision is equal to the relative speed of separation (v2‘ – v1‘) after collision.
Final velocities of the bodies can now be calculated from the above equations.
From equation (IV)
So, in case of elastic collision, the relative speed of approach (v1-v2) before collision is equal to the relative speed of separation (v2‘ – v1‘) after collision.
Final velocities of the bodies can now be calculated from the above equations.
From equation (IV)
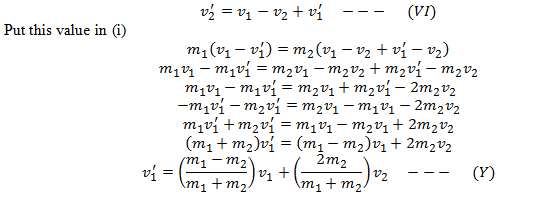 So particle ‘m1’ will go with this velocity after collision.
To find the velocity of ‘m2’ after collision, we consider equation (IV) once more.
So particle ‘m1’ will go with this velocity after collision.
To find the velocity of ‘m2’ after collision, we consider equation (IV) once more.
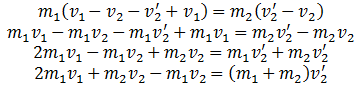
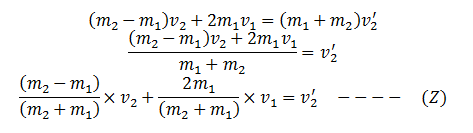 This equation represents the velocity of body m2 after collision.
This equation represents the velocity of body m2 after collision. 
Pingback:index-long-questions-ch3 – msa