Question 2: Explain in detail whether for two vectors of equal magnitudes is it possible to give a resultant of magnitude equal to their individual magnitudes? Justify your answer mathematically.
Answer
As vector is a directed quantity, therefore, its addition depends upon the direction of the vectors to be added. Hence, it is possible that the resultant of two vectors of equal magnitudes yield a vector of the same magnitude provided we look for an appropriate angle between the two vectors.
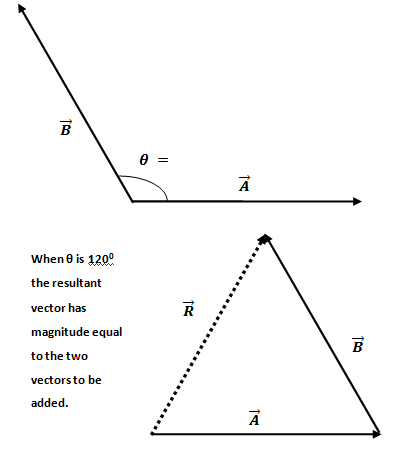
Suppose two vectors ![]() and
and ![]() are to be added.
are to be added.
Let ![]() is acting along the x-axis and
is acting along the x-axis and ![]() is making an angle θ with the x-axis.
is making an angle θ with the x-axis.
Now, in terms of magnitudes only,
Ax = A cos0° and since cos0° = 1, therefore,
Ax = A ———— (1)
Ay = A sin0° . Since sin0° = 0, therefore,
Ay = 0 ———— (2)
Similarly,
Bx = Bcosθ ——— (3)
By = Bsinθ — —– (4)
If ‘R’ is the magnitude of the resultant vector, then,
![]()
Now, putting the values of equations (1), (2), (3) and (4) in this equation,
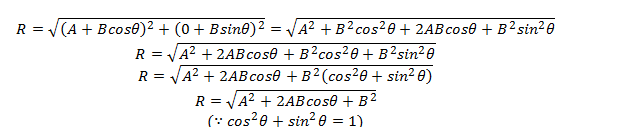
As the magnitude of both vectors is the same, therefore put A = B.
![]()
![]()
Now we have to think about the given condition, i-e, R = A = B and look for some suitable value of θ. The suitable value of θ should be such that the term (1+cosθ) in the above equation gives a value equal to 1/2. So an angle θ for which cosθ = -1/2 would be the appropriate angle. As cos120o is -1/2, therefore, the required angle is 120o.
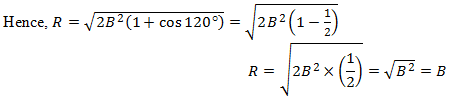
Now A and B are equal as given in the problem, therefore, for θ = 1200 the condition of the problem A = B = R is met.
Thus two vectors of the same magnitudes when added will give a resultant of equal magnitude if the angle between them is 120o. See the figure.

Pingback:Comprehensive Questions, Vectors and equilibrium, Physics 11 … msa
Pingback:Range of possible values of the resultant of two vectors … msa – msa
Pingback:Rectangular components, addition of vectors by rectangular components … msa – msa
Pingback:Definitions and examples of vector and scalar, Physics 11 … msa – msa
Pingback:MCQs on Vectors and Equilibrium, Physics 11 – msa