Question 4: State and explain Gauss’ Law for electrostatics. Also discuss its application with daily life examples.
ANSWER
Gauss’ Law definition
The electric field due to a given charge distribution can be calculated by Coulomb’s law. However, in many cases the calculations become very tough. Gauss’ Law provides us with an alternative method. It states that;
The net electric flux (i-e, the lines of electric field) through a closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space, ε0.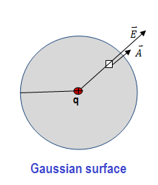
So if the volume within an arbitrary closed surface holds a charge q, then the electric flux φ through the surface is q/ε0.
Mathematically,![]()
Explanation and Mathematical form of Gauss law
We explain the law by computing the flux emerging out from a point charge +q and then for a number of charges or a continuous distribution of charges.
Consider the flux diverging from a point charge q. Consider an imaginary closed spherical surface of radius r with q as its center. Electric flux through an element of area Δ![]() of the sphere is;
of the sphere is;
![]()
Similarly, total flux through the entire spherical surface is,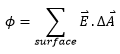
In the present case![]() is radial, and so is the area vector
is radial, and so is the area vector![]() . Therefore, the angle between them is zero. As cos 0o is 1, therefore, for each ∆A,
. Therefore, the angle between them is zero. As cos 0o is 1, therefore, for each ∆A, ![]()
The electric intensity depends upon the distance from the point charge and for a sphere the distance is equal to the radius which is constant for all points of the sphere. So the electric intensity is constant over the sphere.![]()
Now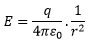
Therefore, φ can be written as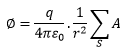
Now surface area of a sphere is 4πr2. Put this value in the above equation,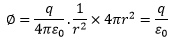
This is the mathematical form of Gauss’ Law.
Now let’s consider the case of point charges, q1, q2… qn inside a closed surface S. The number of lines coming from the these charges will be;
1/ε0(q1+q2+q3+……+qn)
But the number of lines coming out of a closed surface is the sum of the small fluxes over the entire surface. Therefore equating both sides, we get φ described in terms of total charge, Q.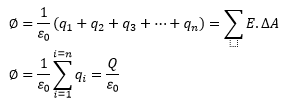
Where Q is the net charge, taking into account the algebraic sign of all charges. If a surface encloses equal and opposite charge, the flux is zero. The flux lines of a negative charge are inward to the closed surface and its flux is negative. This is the mathematical proof of Gauss’s law.
Application of Gauss’ Law
Gauss’s Law is used to find the electric field around a symmetric charge. It has important applications in our daily life as well as the technology we use. Let’s take one such example in detail. Under steady conditions, the electric field E in a metal or a conductor is zero. We know that conductors have a large number of free charges within them. If a resultant field E exists in the conductor, the free electrons will experience a force. They will move and an internal current will set up. After a short time an electrostatic equilibrium is achieved, stopping the current. When no current flows, the resultant force on the electron in the conductor must be zero. Therefore, under electrostatic conditions (i-e, when no field exists within the conductor) the electric field in the interior of a conductor must be zero. Gauss’s law can be applied to show the excess charge on an insulated conductor resides on its outer surface. Consider an insulated conductor carrying excess charge q. Take a Gauss’s surface S inside just below the actual surface of the surface. Under steady conditions, the electric field E in the conductor is zero. Since E=0 in the conductor, therefore, the charge inside S is zero. Therefore, it can be concluded that the charge is outside S, i-e, on the actual surface of the conductor.
To make it simple.
پهٔ یو الیکټریکل کنډکټر کې بلها ډیر فری الیکټران وی. دا الیکټران پهٔ ټول کنډکټر کی ګرځي راګرځي. خو د کنډکټر نه بهر نهٔ شي وتلی. البته که د کنډکټر دواړه غاړو ته د پوټینشل فرق وي نو ډیر پهٔ اسانه پهٔ یو اړخ پهٔ حرکت کی راتلی شي. تر څو چی دا فرق وي ددوي حرکت به جاري وي. او چی کله د پوټینشل دا فرق ختم شي ددوي حرکت هم ودریږي.
بغیر د بهرني پوټنشل ډیفرنس نه، پهٔ کنډکټر کی دننه د فري الیکټرانو پهٔ وجه کرنټ نهٔ پیدا کیږي. دا مونږه د ګاس پهٔ قانون ښودلی شو.
اوس یو بل کیس واخلۍ.
فرض کړۍ پهٔ یو خاص وخت کی پهٔ کنډکټر کی دننه پهٔ یو ځائ د الیکټرانو کمی یا زیاتی راغی. ددی پهٔ وجه به دلته د چارج دباؤ راشي او دغه رنګ پهٔ کنډکټر کی دننه یو الیکټرک فیلډ سیټ اپ شي کوم چی الیکټران پهٔ حرکت کی راولي. پهٔ کنډکټر کی دننه یو اندروني کرنټ پیدا شي. خو لږ وخت پس ښکاره ده چی یو الیکټروسټیټک توازن (یعنی پهٔ ټول کنډکټر کی د چارج یو شان خوریدل) قائم شي. او کرنټ یا د الیکټرانو حرکت ودریږي. داسی حالت کی پهٔ کنډکټر کی دننه الیکټرک فیلډ صفر وي. دغسی په کنډکټر دننه پوټینشل ګریډیئنټ به هم زیرو وي، یعنی د کنډکټر د هر دوه پوایئنټ پهٔ مئینځ کی د پوټینشل فرق زیرو وي.
اوس کهٔ مونږه یو کنډکټر چارج کړو نو څهٔ به کیږي؟ ….. کهٔ مونږه یو کنډنټر ته چارج ورکړو نو په کنډنټر کی چونکه هیڅ پوټینشل ګریډیئنټ یا اییکټرک فیلډ نشته نو دغه ورکړی شوي چارجز به یو بل رِيپل کوي او دغسی به ټول چارج د کنډکټر پهٔ سطح باندِ جمع کیږي او د کنډکټر پهٔ مینځ کی به چارج نهٔ پاتی کیږي.

Pingback:Electrostatics, Physics 12 … msas – msa
Pingback:electric-potential-and-derivation-of-formula-for-electric-potential – msa
Pingback:electric-flux, definition and explanation … msa – msa