Question 3: Show that the energy is conserved in case of SHM.
ANSWER
The law of conservation of energy equally holds in the case of simple harmonic motion. So the KE and PE are mutually converted to one another fully or partly during the course of motion and the sum of P.E and K.E is conserved at any instant during the course of motion. Consider a body of mass ‘m’ attached with a spring of spring constant ‘k’ as shown in the figure. When the body is at rest at point ‘O’, no force acts on it. Fi = 0.
Let the spring is compressed to point ‘A’ by a force Ff such that OA = x0. Then Ff = kx0.
Now the average force is,
Consider a body of mass ‘m’ attached with a spring of spring constant ‘k’ as shown in the figure. When the body is at rest at point ‘O’, no force acts on it. Fi = 0.
Let the spring is compressed to point ‘A’ by a force Ff such that OA = x0. Then Ff = kx0.
Now the average force is,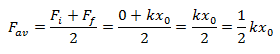 Average work done, W = Fd, is given by
Average work done, W = Fd, is given by This work is stored in the spring as potential energy. Therefore,
This work is stored in the spring as potential energy. Therefore,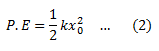 At any point, however,
At any point, however, Similarly, the velocity in case of SHM at any displacement is,
Similarly, the velocity in case of SHM at any displacement is, Therefore,
Therefore, Now
Now 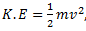 , putting the above value,
, putting the above value,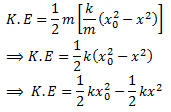 Extreme points A and B
Extreme points A and B
At the extreme points ‘A’ and ‘B’, x = x0, therefore, Therefore, the kinetic energy is zero at the either of the extreme point.
P.E at the extreme points is (equation 2)
Therefore, the kinetic energy is zero at the either of the extreme point.
P.E at the extreme points is (equation 2) Center point
Center point
At the center, x = 0, And potential energy is (equation 2)
And potential energy is (equation 2) Hence we conclude that at extreme points kinetic energy is zero and potential energy is maximum. And at the center, kinetic energy is maximum and potential energy is zero. In between the extreme position and center the energy is partly kinetic and partly potential. When we go from the extreme point toward the center, PE is gradually converting to K.E, till the K.E is maximum at the center and P.E is zero. Then as we go away from the center with maximum K.E and zero P.E, kinetic energy is slowly converting to potential energy until it is maximum at the extreme points where K.E becomes zero. Therefore, total energy remains conserved at any instant.
Hence we conclude that at extreme points kinetic energy is zero and potential energy is maximum. And at the center, kinetic energy is maximum and potential energy is zero. In between the extreme position and center the energy is partly kinetic and partly potential. When we go from the extreme point toward the center, PE is gradually converting to K.E, till the K.E is maximum at the center and P.E is zero. Then as we go away from the center with maximum K.E and zero P.E, kinetic energy is slowly converting to potential energy until it is maximum at the extreme points where K.E becomes zero. Therefore, total energy remains conserved at any instant.
ANSWER
The law of conservation of energy equally holds in the case of simple harmonic motion. So the KE and PE are mutually converted to one another fully or partly during the course of motion and the sum of P.E and K.E is conserved at any instant during the course of motion.
 Consider a body of mass ‘m’ attached with a spring of spring constant ‘k’ as shown in the figure. When the body is at rest at point ‘O’, no force acts on it. Fi = 0.
Let the spring is compressed to point ‘A’ by a force Ff such that OA = x0. Then Ff = kx0.
Now the average force is,
Consider a body of mass ‘m’ attached with a spring of spring constant ‘k’ as shown in the figure. When the body is at rest at point ‘O’, no force acts on it. Fi = 0.
Let the spring is compressed to point ‘A’ by a force Ff such that OA = x0. Then Ff = kx0.
Now the average force is,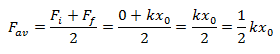 Average work done, W = Fd, is given by
Average work done, W = Fd, is given by This work is stored in the spring as potential energy. Therefore,
This work is stored in the spring as potential energy. Therefore,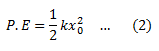 At any point, however,
At any point, however, Therefore,
Therefore, Now
Now 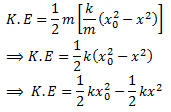 Extreme points A and B
Extreme points A and B
At the extreme points ‘A’ and ‘B’, x = x0, therefore,
At the center, x = 0,
 And potential energy is (equation 2)
And potential energy is (equation 2)
Pingback:free-and-forced-oscillations – msa
Pingback:projection of a body in circular motion executes SHM … msa – msa
Pingback:mcqs-chapter-7-p-11 – msa
Pingback:index-lq7-p11 – msa
Pingback:Comprehensive Questions, Oscillation, Physics 11 (new course) … msa – msa