
Select the correct answers of the following questions.
1. Tuning of a radio set is an example of
| (a) Mechanical resonance | (b) Musical resonance | (c) Electrical resonance | (d) Free vibration |
Explanation: see Conceptual Question 1.
2. The heating and cooking of food evenly by microwave oven is an example of
| (a) S.H.M | (b) Resonance | (c) Damped Oscillation | (d) Free oscillation |
3. The periods of the same pendulum at Karachi and Murree are related to
| (a) Tk > TM | (b) TK < TM | (c) TK = TM | (d) 2TK = 3TM |
Explanation: Time period of a simple pendulum is given by
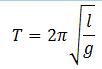
Therefore, time period of a pendulum depends on the gravitational acceleration, g. However, g depends upon the height from the center of the earth. Height of Karachi is about 500 m whereas height of Murree is 2291 m. Therefore, g has smaller value in Murree than Karachi. As T is inversely proportional to g, therefore, the time period of the same pendulum will increase in Murree.
4. In an isolated system the total energy of vibrating mass spring system is
| (a) Variable | (b) low | (c) high | (d) constant |
Explanation: See Comprehensive Question 3.
5. While deriving the equation of time period of simple pendulum which quantity should be kept small?
| (a) Length of simple pendulum | (b) Amplitude | (c) Mass of the bob | (d) gravitational acceleration g |
Explanation: The time period of a pendulum depends upon the length of the pendulum and local value of the gravitational acceleration, g. However, for larger angles, the time period has a smooth deviation from this equation. Therefore, for deriving accurate results for the time period, the angle (i-e, amplitude) should be kept small.
6. If the period of oscillation of mass M suspended from a spring is 2 s, then the period of mass 4M will be
| (a) 1 s | (b) 2 s | (c) 3 s | (d) 4 s |
Solution: If k is the spring constant and M is the mass suspended, then time period of the system is
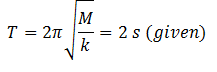

Put the value of M’ = 4M and simplify to get
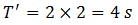
7. The time period of a simple pendulum is 2 seconds. If its length is increased by 4 times, then its period becomes
| (a) 16 s | (b) 12 s | (c) 8 s | (d) 4 s |
Solution: Let l is the length of the pendulum and g is the local value of gravitational acceleration, then
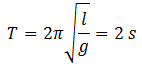
If the length is increased 4 times, then
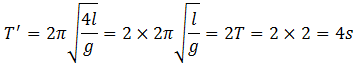
8. To make the frequency double of a spring oscillation, we have to
| (a) Reduce the mass to one-fourth | (b) Quadruple the mass | (c) Double the mass | (d) Half the mass |
Solution: If M and k are the mass and spring constant, then
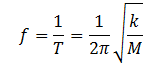
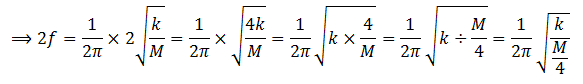
Therefore,
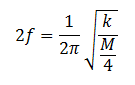
Double the frequency, the mass is reduced to one-fourth.
9. The restoring force of SHM is maximum when particle
| (a) Displacement is maximum | (b) Half way between them | (c) Crossing mean position | (d) At rest |
Solution: Try yourself. (Hint: F = kx)
10. Two springs of constants K1 and K2 are joined in series. The effective spring constant of the combination is given by

Solution: We have to make use of some theory and a lot of math. Since
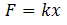
Therefore, both springs will compress to different distances as their constants are different. The force is same (F) for both springs connected in series, therefore,
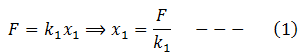
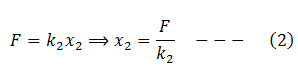
When the springs are connected in series and the force F is applied, x is the displacement, such that
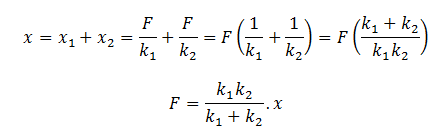
Compare with the equation of spring F = kx and get, Effective spring constant of the combination
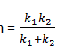
11. In a garden a boy is swinging in the standing position. How will the time period of the swing be affected if the boy sits down on the swing?
| (a) Time period will not change | (b) Time period will increase | (c) Time period will decrease | (d) Time period will depend on the weight of the boy |
Explanation: When the boy is standing, his center of gravity is up in the body. When he sits the center of gravity lowers. It increases the effective length of the swing. With the increase in l, the time period increases.
Any feedback? ….. Please text on 03488519873


Pingback:numerical-problems-on-oscillation-physics-11-msa – msa
Pingback:Comprehensive Questions on Oscillation, Grade 11 … msa – msa
Pingback:Physics 11 (New Course) – msa
Pingback:Numerical Problem 11, Oscillation, Physics 11 – msa
Pingback:numerical-problem-1-oscillation-physics-11-msa – msa