Question 2:What does a unit system mean? Give names of three different systems of units. In System International, explain what is meant by base unit?

Answer

Physics is the science of measurements. By measurement, we mean a direct or indirect comparison of a certain quantity with an appropriate standard of measurement, called unit (more precisely, a unit is a standard by which a dimension can be numerically expressed).

System of units

• • 1. A system of units is a class of units made from a base set of units such that every case of the class is a standard unit for a physical dimension and every physical dimension has an associated unit.
       

       Explanation    Suppose we have one set of many physical quantities. Suppose we have another set of many units. This set of units is formed by some base and many other derived units. Now, if all physical quantities in the first set have a specific unit in the second set, then the second set is called the system of units for the quantities in the first set.

    2. An equivalent statement of the system of units is a system of units is a set of fundamental units that is sufficient for measuring the properties of a class of quantities under consideration.

Three systems of measurements

There are many systems of units, developed according the needs and environment of the people living in different parts of the world. However, most of them were not suitable for the scientific work. Scientific work needed a convenient and simple system. Initially, in scientific work, the following three systems of units established their importance. They define the three fundamental quantities, mass, length and time, in their respective units.

MKS system of units

Meter (M), Kilogram (K) and Second (S) are the units of length, mass and time, respectively in this system.

CGS system of units

Centimeter (C), Gram (G) and Second (S) are the units of length, mass and time in this system. This system of units is used when we are concerned with relatively small quantities.

FPS system of units

Foot (F), Pound (P) and Second (S) are used for the measurement of the base quantities length, mass and time. This system of units is also called British Engineering System.

It should be noted that in these systems only three quantities, length, mass and time, are considered the base quantities.

SI and base units

System International (SI)

In 1960, the General Conference on Weights and Measures (an international committee) agreed on a set of definitions and standards to describe the physical quantities. The system that was established is called System International (SI). Due to its simplicity and convenience in measurement, the world’s scientific community now globally uses it.

Base units in SI

SI consists of seven base units. These seven base units are the building blocks from which the derived units are constructed. Base units are not related to one another and they do not depend on each other for their definitions. They are used to determine the expressions for the derived units in terms of base units.

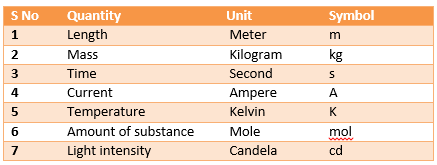Table of Base Units

Derived units

Units obtained by the multiplication and/or division (ratios) of base units units are called Derived Units.

Few commonly used derived units are as follow;

Table of Base Units

Derived units

Supplementary Units

The international committee (General Conference on Weights and Measures) has not yet classified plane angle and solid angle under base units or derived units. These are called supplementary units. These are dimensionless quantities.

• • • Radian is the unit of plane angle represented by symbol “rad”.
    • Steradian is the unit of solid angle represented by “sr”.

Radian

Though degree is the familiar unit of plane angle, but plane angle is usually measured in radians. A radian is defined as “a plane angle subtended at the center of a circle by an arc equal to the length of the radius of the circle.”

In the figure on the right, we have

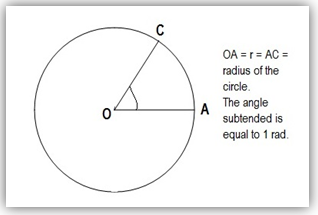
m AC = m OA= radius of the circle.Therefore, m∠AOC = 1 rad

If s is the arc which subtends an angle θ at the center of a circle of radius r, then,

θ = (s/r) rad

As‘s’ and ‘r’ both are lengths, θ is a number without having any dimensions.

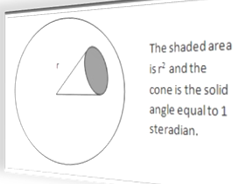
Steradian

Steradian is defined as “the solid angle subtended at the center of a sphere by an area of its surface equal to the square of the radius of that sphere.”

As the surface area of a closed sphere is 4πr², therefore, the solid angle subtended by a closed sphere at its center is = 4πr²/r² = 4π sr

 

See more