Q 1: A charge Q is divided into two parts q and Q-q and separated by a distance R. The force of repulsion between them will be maximum when:

(a) q = Q/4

☛(b) q = Q/2

(c) q = Q

(d) none of these

Solution

The electrostatic force between the charges is given by

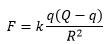
Now the electrostatic force will be maximum for the maximum value of the product q (Q-q).

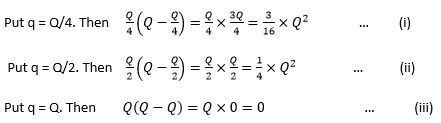
Now compare (i), (ii) and (iii), we see that 1/4 > 3/16 > 0. Therefore, the force is maximum for q = Q/2 in the three options. Since Q/4 is less than Q/2 and Q is greater than Q/2, therefore, we conclude that the force will be less for any value of q less than or greater than Q/2. (You can check it!). Therefore, the fourth option (none of these) is also incorrect and the force is maximum for q = Q/2.

Q 2: Some charge is being given to a conductor. Then its potential:

Explanation

When charge is given to a conductor, it equally distributes on the surface. Inside the conductor, the electric field intensity is zero. Since E = -ΔV/Δx, so E = 0 ⇒ Δ V = 0. Therefore, the potential inside the conductor is constant. Since the extra charge symmetrically distributes on the surface of the conductor, therefore, the potential on the surface and inside the conductor will be same. Therefore, potential remains same throughout the conductor.

(a) is maximum at the surface

(b) is maximum at the center

☛(c) remains same throughout the conductor

(d) is maximum somewhere between the surface and the center

Q 3: Electrical potential of earth is taken to be zero because the earth is good:

(a) semiconductor

☛(b) conductor

(c) insulator

dielectric

Explanation
By convention, the electrostatic potential of earth is taken to be zero because it is a good conductor.

Q 4: A proton is about 1840 times heavier than an electron. When it accelerated by a potential difference 1 KV, its kinetic energy will be:

1840 keV

1/1840 keV

☛(c) 1 keV

(d) 920 keV

Explanation: One electron volt is the energy gained by an electron falling through a potential difference of ∆V = 1 V. The energy gained by any charge e is, therefore, U = e∆V. Thus it depends upon the charge of the particle and not the mass. As electron and proton has the same charge, therefore, the proton would have its K.E = 1 keV when accelerated through a potential difference of 1 KV.

Q 5: A capacitor is charged with a battery and then it is disconnected. A slab of dielectric is now inserted between the plates then:

(a)The charge on the plates reduces and the potential difference decreases

(b) Potential difference between the plates increases, stored energy decreases and charge remains the same

☛(c) Potential difference between the plates decreases, stored energy decreases and charge remains unchanged

(d) none of theses

Explanation: When a dielectric is introduced between the charged plates of the capacitor, the electric field between the plates causes the nuclei of the dielectric slightly shifted towards the negatively charged plate and the electrons towards the positively charged plate. The electric field caused by the polarized dielectric is opposite to the electric field between the capacitors. Therefore, the net value of the electric field decreases. Since V = Ed; the potential difference also decreases with the electric field. Similarly, the electrical potential energy stored in the capacitor is U = 1/2(CV²). So with the decrease in the potential difference, the stored energy also decreases. On the other hand cumulative charge on the plates remains unchanged because there is no flow of charge in the system of the capacitor. Also see comprehensive questions no 6 and 8.

Q 6: A one microfarad capacitor of a TV is subjected to 4000 V potential difference. The energy stored in the capacitor is:

☛(a) 8 J

(b) 16 J

(c) 4 × 10-3 J

(d) 2 × 10-3 J

Solution: C = 1 μF,     V= 4000 V,                 U = ½ CV² = ½ * 1 * 10^-6 * 4000 * 4000 = 8 J

Q 7: In the fig below, the charge on 3µF capacitor is:

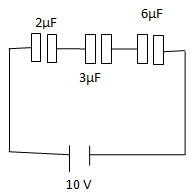
(a) 5µC

☛(b) 10 µC

(c) 3 µC

(d) 6 µC

Solution: In the series combination of capacitors,

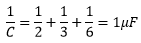
Now Q = CV = 1 * 10 = 10 μC (Note: Equal charge gathers on all plates).

Q 8: The electric potential between two points A and B is ΔV. The work done W by the field in moving a charge Q from A to B is:

(a) W = -qΔV

☛(b) W = qΔV

(c) W = -ΔV/q

(d) W = ΔV/q

Explanation: See definition. Comprehensive question 5.

Q 9: The electric flux through the surface of a sphere due to charge q placed at its center depends upon:

(a) radius of the sphere

(b) quantity of charge outside the sphere

(c) surface area of the sphere

☛(d) The quantity inside the sphere

Explanation: See Gauss law. The electric flux through a closed surface is equal to the total charge included by the surface divided by the permittivity of the free space.

Q 10: Two parallel metal plates are at a distance of 8.00 m apart. The electric field between the plates is uniform directed toward the right, and has a magnitude of 4.00 N/C. If an ion of charge +2e is released at rest to the left-hand plate, what is its kinetic energy when it reached the right-hand plate?

(a) 4 eV

☛(b) 64 eV

(c) 32 eV

(d) 16 eV

Solution: K.E = q∆V = 2eEd = (2*8*4) eV = 64 eV.