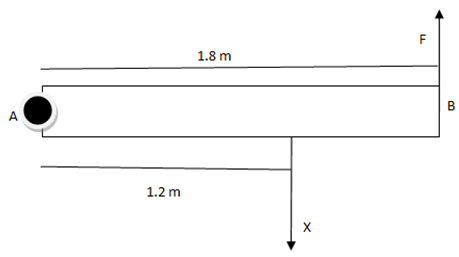
Problem 11: The diagram below shows the plan view of a door hinged at A. If a man applies a force F of 40 N at the end marked B, calculate the moment of this force about A. What is the minimum force X that must be applied at C in order to stop the door from turning? Name the principle applied to solve this problem.
Solution
Given data
Force applied
by the man to turn the door = F = 40 N
Width of the door, AB = moment arm = 1.8 m
Force applied to stop this torque = X
Point at which X acts = C
Moment arm of X = AC = 1.2 m
Required
Moment of the force (torque) about A, τ =?
Force applied at C = X =?
Now
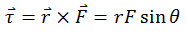
Where ‘r’ is the moment arm and θ is the angle between moment arm and the force, which is 900 in this case. Since sin 900 = 1, therefore,
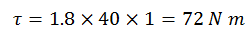
To stop this torque the force X must produce a torque of the same magnitude in the opposite direction. Therefore,
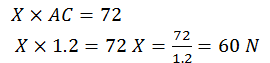
So a force of 60 N must be applied at point C to stop the action of torque by the man.
The principle used is a body remains in equilibrium when the vector sum of torques acting on it is zero.
Can you say in this problem, why a force of 60 N is required to cancel a torque produced by 40 N of force?

Pingback:numerical-problem-10-chapter-2-physics-11 – msa
Pingback:Numerical on Vectors and Equilibrium, Physics 11 – msa