Select the correct answers of the following questions.
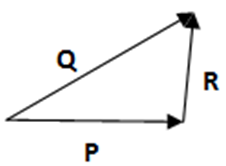
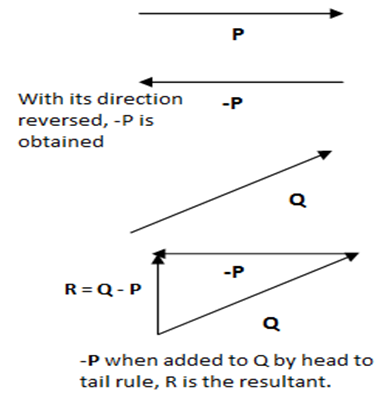
1. Which is a correct equation for vector R?
(i) R = P – Q (b) R = Q – P (c) R = P + Q (d) none
Solution: Take the negative vector of P and add with Q by head-to-tail rule.
(ii) Which of the following represents a vector and a scalar respectively?
| Options | Vector | Scalar |
| A | Speed | Velocity |
| B | Acceleration | Deceleration |
| C | Force | Power |
| D | Work | Density |
Please note: (A) Not in order, speed is scalar and velocity is vector. (B) Both vectors (D) both scalars.
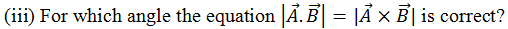
(a) 300 (b) 450 (c) 600 (d) 900
Solution: We are concerned with the magnitudes of scalar and vector products of the two vectors. Since the scalar and vector multiplications differ only in the difference of the sine and cosine values of the angle between them, therefore, if the angle between the vectors is such that both its sine and cosine values are equal, the magnitudes of the scalar and vector product of such vectors will also be equal. Now, 450 is the angle whose sine = cosine = 1/√2, therefore, if two vectors are making 450 angle between them, the magnitudes of the scalar and vector products of such vectors will be equal.
(iv) The following diagrams show a uniform rod with its midpoint on a pivot. Two equal forces F are applied to the rod, as shown. Which diagram shows the rod in equilibrium?
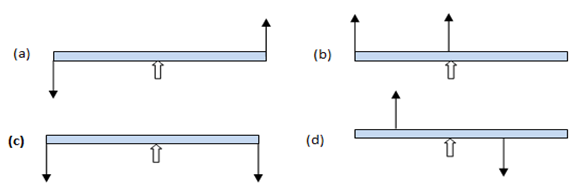
Explanation: Please note a body is in equilibrium when the resultant of all forces acting on it is zero and the sum of all torques acting on the body is zero.
(a) Anti-clockwise torque (b) clockwise torque (c) no torque (both torques cancel each other)
(d) Anti-clockwise torque. Hence (c) is the correct option.
(v) Which of the following instrument work on the principle of moments?
(a) Physical Balance (b) Spring Balance (c) Measuring Cylinder (d) Vernier Calipers
(Note: A physical balance works like option c in the previous MCQ. When the balance is in equilibrium, the forces on both sides are equal implying the masses to be equal.)
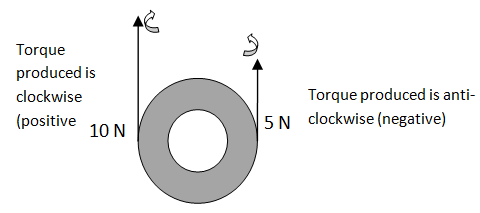
(vi) What is the torque acting on the wheel of radius 2 m?
(a) 10 N anti-clockwise (b) 10 N m anti-clockwise (c) 10 N m clockwise
(d) 5 N m clockwise
Hint: The force 10 N is producing a clockwise torque. Take it as negative. The 5 N force is producing anti-clockwise torque. Take it positive. Apply the formula and find both torques. Then add them. Remember the anti-clockwise torque is positive. Angle Θ in both cases is 90o.
(vii) Find the mass of the rod as shown in the figure below. Its center of gravity is 14 m from the end A.
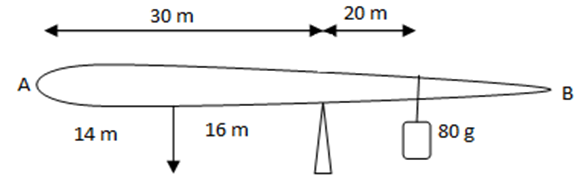
(a) 100 g (b) 150 g (c) 80 g (d) 5 g
Solution: Clockwise torque produced by 80 g (= 0.08 kg) mass to the right = 20 * 9.8 * 0.08 = 15.68 N m
Let m be the mass of the rod, then the anti-clockwise torque produced by the weight mg to the left = 9.8m*16 = 156.8 m. Since the rod is in equilibrium, both torques’ are equal.
156.8 m = 15.68 N m OR m = 15.68/156.8 = 0.1 kg = 100 g
vii: The diagram shows four forces applied to a circular object. Which of the following describes the resultant force and resultant torque on the object?
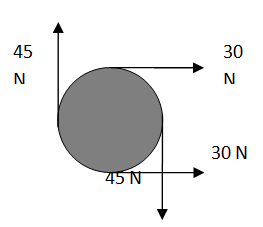
| No | Resultant Force | Resultant Torque |
| A | Non-zero | Non-zero |
| B | Non-zero | Zero |
| C | Zero | Non-zero |
| D | Zero | Zero |
Hint: Both the 45 N forces produce torque. Torques due to 30 N forces cancels.
Forces of 45 N cancel each other. Forces of 30 N have a resultant of 60 N.
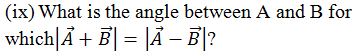
(a) 300 (b) 450 (c) 600(d) 900
Solution: Consider the following diagram. A and B are two forces making angle 900 between them. When added and subtracted the magnitudes of the resultants are equal.
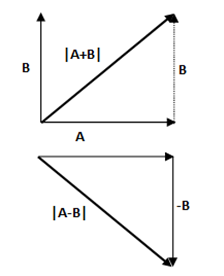
(x) The sum of magnitudes of two vectors is 16 N. If the resultant force is 8 N and its direction is perpendicular to minimum force then the forces are:
(a) 6N and 10 N (b) 8N and 8 N (c) 4 N and 12 N (d) 2 N and 14 N
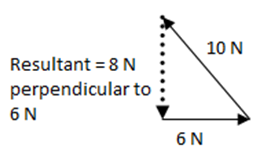
Solution: Let x1 and x2 are the magnitudes of two vectors such that x1<x2 . Now if the resultant force is perpendicular to x1, then the three vectors when combined make a right angled triangle as shown in the figure. We know that for a right angled triangle,
(Hypotenuse)2 = (base)2 + (perpendicular)2
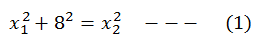
Given in the problem is
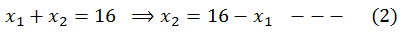
Put this value of x2 in equation (1)
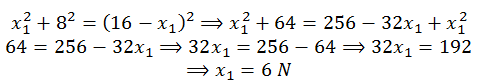
Put x1 = 6 in equation (2), we have x2 = 16 – 6 = 10 N
(xi) A person walks first 10 km north and 20 km east then the resultant vector is;
(a) 22.36 km (b) 22.46 km (c) 25.23 km (d) 36 km
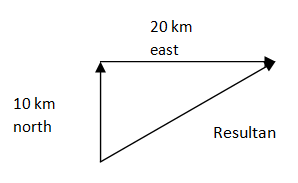
Hint: The distance vectors the person covers are towards north and east, perpendicular to one another. The schematic diagram of the problem is a right angled triangle. Solve for the of the triangle as,
(Base)2 + (perpendicular)2 = (hypotenuse)2

Pingback:numerical-problem-11-chapter-2-physics-11 – msa
Pingback:Ship movement from P to R – msa
Pingback:Index Conceptual Questions, Vectors and Equilibrium … msa – msa
Pingback:Numerical on Vectors and Equilibrium, Physics 11 – msa
Pingback:Comprehensive Questions, Vectors and equilibrium, Physics 11 … msa – msa