Question 6: In what region of space is the potential due to a uniform closed sphere the same as that of a point charge? In what region it differs from that of a point charge?
ANSWER
According to Coulomb’s law the electric potential due to a point charge at a distance r is,
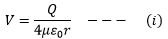
Now consider the case of a sphere of radius R on which the charge is uniformly distributed. As the charge is spherically symmetric, we apply Gauss’s law. Enclose the sphere in a closed concentric surface of radius of r > R. Since the charge enclosed by the surface is the charge on the given charged sphere, therefore, it acts like a point charge and the potential on the closed surface is same like a point charge, that is,
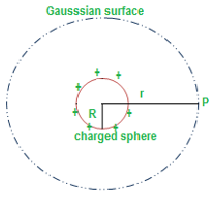
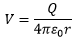


Pingback:relation-of-volt-and-electron-volt – msa
Pingback:non-uniform-charge-and-point-charge – msa
Pingback:index-sq11-p12 – msa