Show that the satellite near the earth will have greater velocity.

ANSWER

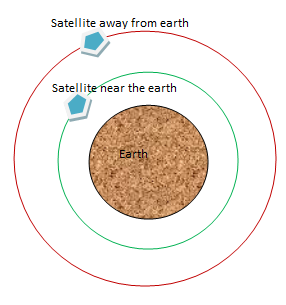
A satellite moves in a circular orbit around the planet (earth) with constant speed depending on the mass of the satellite and its distance from the center of the planet (earth). Its path is a circle of constant radius around the earth. The necessary centripetal force is provided by the gravity in order to keep the body in the circle.
Suppose, M_e is the mass of earth, m_s is mass of the satellite and G is the gravitational constant, then the centripetal force is given by,

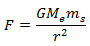
The centripetal acceleration caused by this force is .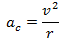

Using Newton’s second law of motion, we have for the motion of satellite,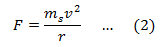

Both these forces are same, hence equating them,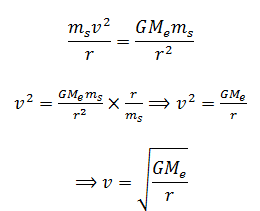

This means the velocity of the satellite will be greater if ‘r’ is small. Since, ‘r’ is the distance of the satellite above the earth, therefore, the satellite near the earth (When ‘r’ will be less than when it is away from the earth) will move faster than if it is farther from the earth.