Question 3: Show that the role playing by mass in linear motion is same as the role playing by moment of inertia in rotatory motion.

ANSWER

Role of mass in linear motion

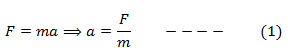
We know that in the case of linear motion, This equation means that linear acceleration is inversely proportional to the mass of the body. If a certain force has to change the state of rest or uniform velocity of a body, mass is the determining factor. Larger the mass more difficult it is to change its state of rest or uniform motion. So mass is the measure of the inertial property of the body.

Role of moment of inertia in circular motion

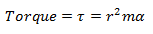
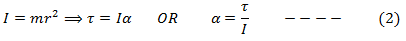
Similarly, in the case of angular motion, r = radius of the circle m = mass of the body α = angular acceleration of the rotation Now Equation (2) clearly indicates that angular acceleration is inversely proportional to the moment of inertia. For a certain torque (rotating force), the angular acceleration is dependent on the mass times square of radius (I = moment of inertia = mr²). Larger the moment of inertia more difficult it is to change the state of uniform angular velocity of the body. This is exactly the same role mass plays in linear momentum. (Equation 1)