Question 11: A current carrying loop, free to turn, is placed in a magnetic field B. What will be its orientation relative to B in the equilibrium state?
ANSWER
Suppose a loop with cross-sectional area A and carrying a current I is placed in a magnetic field B. Further, let the plane of the loop is making an angle θ with B.
Now consider the current moving in the loop. In opposite sections of the loop, the direction of current is opposite to one another. If current flows up (for example) in a segment of loop, then in the part opposite to this segment current will be flowing down.
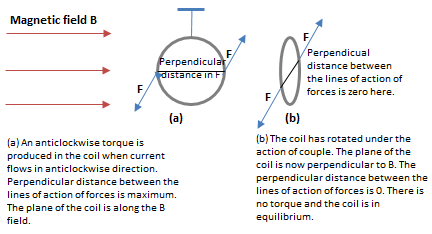
The direction of force on current carrying loop due to the magnetic field depends upon the direction of the flow of the current. The forces on the opposite sections of the loop, therefore, would be opposite to one another. Hence, a torque will produce and the loop will rotate. This torque is mathematically given as
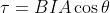
θ is the angle between the direction of flow of current and magnetic field B.
Under of this torque the loop will rotate. This rotation will also change the angle θ and a stage will come when it is 90°. The torque will be zero then, as cos 90° = 0. In such a position the plane of the loop is perpendicular to B. At this position no force would be acting on the loop, no torque would produce and the loop would be in equilibrium.

Pingback:index-Conceptual Questions on Electromagnetism … msa – msa
Pingback:A current-carrying coil behaves like a bar magnet … msa – msa
Pingback:neutron-in-a-cyclotron – msa