Each of the following questions is followed by four answers. Select the correct answer in each case.
(2) Three resistors of resistance R each are combined in various ways. Which of the following cannot be obtained?

Answer: Correct option is (b).
Solution: We try various combinations and find which of the options is not possible.
(i) All resistors in series. It gives equivalent resistance, Req = R+R+R = 3R.
It is option (a).
(ii) All resistors in parallel.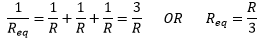
This is option (c).
(iii) Two resistors in parallel and one in series. Equivalent resistance of parallel resistors is
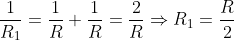
Equivalent resistance of the whole circuit is, then
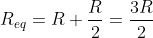
It is not included in the given options.
(iv) Two resistors in series, one in parallel.
Equivalent resistance of series resistors is R + R = 2R
Equivalent resistance of the circuit
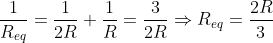
This is option d. Therefore, (b) is the correct option.
(3) Calculate current in 2 Ω resistance.
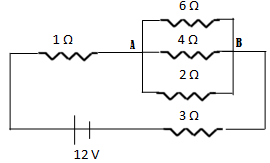
(a) 1 A (b) 1.29 A (c) 0.73 A (d) 1.43 A
Solution
Equivalent resistance of the 3 parallel resistors is
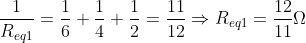
This resistance is now in series with the remaining 2 resistors. Therefore, equivalent resistance of the circuit
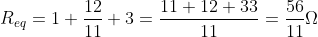
Apply Ohm’s law to find current in the circuit.
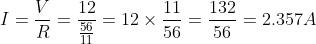
Similarly, potential drop across A and B is
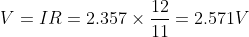
Therefore, current in 2 Ω resistor is
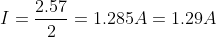
(4) 106 electrons are moving through a wire per second. The current developed is
(a) 1.6 * 10-19 A (b) 1 A (c) 1.6 * 10-13 A (d) 106 A
Solution
Current is the flow of charge per second and one electron bears 1.6 * 10-19 C of charge. Thus 106 electron have a charge = 1.6 * 10-19 * 106 = 1.6 * 10-19+6 = 1.6 * 10-13 C of charge. As this much charge flows in one second, therefore, it is the current developed.
(5) When a wire is stretched and its radius becomes r/2, then its resistance will be
(a) 16 R (b) 4 R (c) 2 R (d) 0
Solution
When a wire is stretched, its length increases and cross-sectional area decreases. In the given problem the wire is stretched to the extent that its radius becomes half of the original radius of the wire. With the decrease in the radius, the cross-sectional area of the wire also decreases. Let original radius of the cross-sectional area A of the wire is ‘r’. Therefore area of the cross-section is A =πr2
Let its resistance is R, then
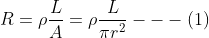
Now when the wire is stretched and the radius becomes r/2, then its cross-sectional area is
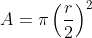
Therefore, its resistance will be
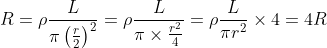
(By putting the value of R from equation 1).
(6) A wire of uniform cross-section A, length L and resistance R is cut into two equal parts. The resistivity of each part will be
(a) Doubled (b) halved (c) remains the same (d) one fourth
Explanation: Resistivity of a conductor is defined as the resistance of unit cube of the conductor. It remains same at a particular temperature irrespective of the length of the conductor. So resistivity is different from resistance.
(7) The resistivity of two wires is ρ1 and ρ2 which are connected in series. If their dimensions are same then the equivalent resistivity of the combination will be
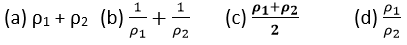
Explanation: Equivalent resistivity of the conductors in the problem will be equal to the average of the resistivity of the conductors which is given in option (c).
(8) The power (See electric power in Urdu) of two electric bulbs are 100 W and 200 W which are connected to the power supply of 220 V. The ratio of the resistances of their filaments will be
(a) 1:2 (b) 2:1 (c) 1:3 (d) 4:3
Solution
Try to solve it.
Hint: Use formula, Power = P = VI and find currents I1 and I2 in the two bulbs. Then find the resistances of the bulbs R1 and R2 by using the formula R = V/I. Find R1/R2. It should be 2/1.
(9) Thermocouple is an arrangement of two different metals
(a) To convert heat energy into electrical energy (b) To produce more heat
(c) To convert heat energy into chemical energy (d) To convert electric energy into heat energy.
Explanation: See theory of thermocouple (Question 8, comprehensive questions).

I am very glade to see such a informative m.c.q. Sir are you write any m.c.q book of a physics. If yes then tell me about the book name,and it’s availability?
Irfan
Sorry, we do not publish books. However, soo we will be uploading solved mcqs included in the ETEA tests during the last few years. However, this will take some time.
Pingback:numerical-problems-electricity-chapter-2-physics-12 – msa
Pingback:index-sq-ch2-p12 – msa
Pingback:Comprehensive Questions, Current Electricity … msa – msa
Pingback:Numerical Problem 11, Current Electricity, msa – msa
Sir Thank You!
You are welcome, Hamza.
Jazak Allah khiran …..sir may Allah bless you… sir in question ko is website sa khatam ni krna beshak books change ho gie hn…..it will help the improvers
Daim Ali
In sha Allah, will not delete the pages even if the courses change.
Thank you for taking interest.
Pingback:Physics 12 – msa
Pingback:numerical-problem-1-current-electricity-chapter-2-physics-12 – msa