MCQs on Vectors and Equilibrium, Physics 11

Multiple Choice Questions, Vectors and Equilibrium

Choose the best possible answer;

Two vectors lie with their tails at the same point. When the angle between them is increased by 20° their scalar product has the same magnitude but changes from positive to negative. The original angle between them was:

(A) 0 (B) 60° (C) 70° (D)80°

Solution: A.B = ABcosθ = ABcos 80° = 0.174AB. When the angle is increased by 20° the new angle is 100°. So, A.B = ABcos100° = 0.174AB.
The minimum number of vectors of unequal magnitudes required to produce zero resultant is

(A) 2 (B) 3 (C) 4 (D)5

Solution MINIMUM NUMBER OF UNEQUAL VECTORS TO GIVE NULL VECTOR: On the minimum, three unequal vectors will give a zero resultant (or null vector). The resultant is said to be zero or null if the vectors being added forms a close shape when put head to tail. So three vectors of unequal magnitudes when put head to tail and they form a triangle (triangle is a close shape), the resultant is a null vector. In the diagram three vectors A ,B and C are added by head-to-tail method. The resultant vector is zero.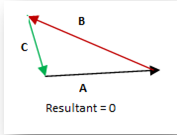 Note that two vectors can also give a zero resultant if they are equal and anti-parallel. However, the condition of the problem demands the vectors to be unequal. Therefore, we can’t take the case of two vectors.
If the resultant of two vectors, each of magnitude A is also a vector of magnitude A, the angle between the two vectors will be

(A) 30° (B) 45° (C) 60° (D)120°

Solution: See solution here.
The magnitude of vector A = 2î + ĵ + 2k̂ is

(A) 9 (B) 5 3 (D) 1

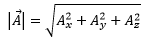
Solution: The magnitude of vector A in space is Here AX = 2, AY = 1, AZ = 2, therefore,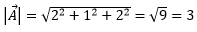
When Fx = 3 N and F = 5 N then Fy =

(A) 6 N (B) 4 N (C) 2 N (D) 0 N

Solution:
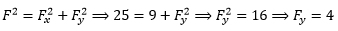
A meter stick is supported by a knife edge at the 50 cm mark. Asif hangs masses of 0.4 kg and 0.6 kg from the 20 cm and 80 cm marks respectively. Where should Asif hang a third mass of 0.30 kg to keep the stick balanced?

20 cm (B) 70 cm (C)30 cm (D)25 cm

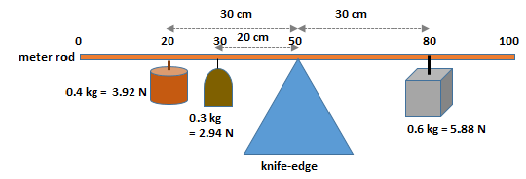
Solution: See the diagram below. Clockwise torque = 5.88 × 0.3 = 1.674 N m … (A) Counterclockwise torque = 3.92 × 0.3 = 1.176 … (B) Difference in torques = 1.764 – 1.176 = 0.588 N m So we need 0.588 N m torque in the counterclockwise direction from a mass of 0.3 kg = 2.94 N. Therefore, if x is the distance from the point of balancing, then 2.94x = 0.588 ⇒ x = 0.588/2.94 = 0.2 m. Hence the third mass should be hung 0.2 m = 20 cm from the point of balancing. As the point of balancing is at 50 cm, therefore, the mass should be hung on 30 cm mark.
A_x = 1.5 cm, A_y = -1.0 cm, into which quadrant do the vector A point?

(A) I (B) II (C) III IV

Explanation: Since the y-component is negative and x-component is positive, the vector points in the IV quadrant. (Draw the vector according to the scale).
A.(A × B) = …

(A) 0 (B) 1 (C) AB (D) A²

Explanation: Let A × B = C. Now C is perpendicular to both A and B. Now as A.C = AC cosθ = AC cos90° and cos90° = 0. Therefore, option A is correct.
Two forces of magnitudes 20 N and 50 N act simultaneously on a body. Which one of the following cannot be the resultant of the two forces?

(A) 20 N (B) 30 N 40 N (D) 70 N

Explanation: If A and B are two vectors to be added, then depending on the angle between them, the magnitude of the resultant is either equal to or less than A + B and greater than or equal to A – B. Now the sum of magnitudes of the given vectors is 20 + 50 = 70 and difference is 50 -20 = 30. Therefore, the range of the sum is from 30 to 70 N. Only 20 N is out of this range. Therefore, A is the correct option.
If the dot product of two non-zero vectors A and B is zero, then the magnitude of their cross product is

(A) 0 (B) 1 (C) AB (D)-AB

Explanation: A.B = ABcosθ, and since A and B are nonzero, therefore, cosθ = 0 ⇒ θ = 90°. Now A X B = ABsinθ = ABsin90° = AB. (∵ sin90° = 1).
11. The sum of magnitudes of two forces is 16 N. If the resultant force is 8 N and its direction is perpendicular to minimum force the force are

(A) 6 N and 10 N (B) 8 N and 8 N (C) 4N and 12N (D) 2 N and 14 N

Solution: Let x₁ and x₂ are the magnitudes of two vectors such that x₁ is less than x₂. Now if the resultant force is perpendicular to x₁, then the three vectors when combined make a right angled triangle as shown in the figure.

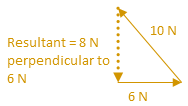
We know that for a right angled triangle, (Hypotenuse)² = (base)² + (perpendicular)².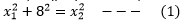

Given in the problem is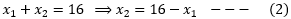

Put this value of x₂ in equation (1)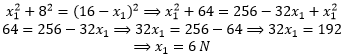

Put x₁ = 6 in equation (2), we have x₂ = 16 – 6 = 10 N
Find the mass of the uneven rod shown in the figure. If its center of gravity is 14 cm from end A.

(A) 100 g (B) 150 g (C) 80 g (D) 5 g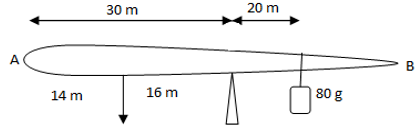

SOLUTION: Clockwise torque produced by 80 g (= 0.08 kg) mass to the right = 20 × 9.8 × 0.08 = 15.68 N m.
Let m be the mass of the rod, then the anti-clockwise torque produced by the weight mg to the left = 9.8m × 16 = 156.8m N m. Since the rod is in equilibrium, both torques are equal. 156.8m = 15.68 OR m = 15.68/156.8 = 0.1 kg = 100 g.
The following diagrams show a uniform rod with its midpoint on the pivot. Two equal forces F are applied on the rod as shown in the figure. Which diagram shows the rod in equilibrium?

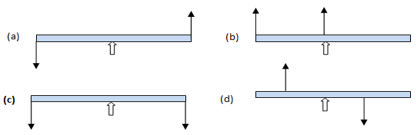
Solution: Please note a body is in equilibrium when the resultant of all forces acting on it is zero and the sum of all torques acting on the body is zero.
(a) Anti-clockwise torque (b) clockwise torque (c) no torque (both torques cancel each other) (d) Anti-clockwise torque.
Hence (c) is the correct option.
For which angle the equation

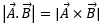
is correct?

(A) 30° (B) 45° (C) 60° (D) 90°

Solution: We are concerned with the magnitudes of scalar and vector products of the two vectors. Since the scalar and vector multiplications differ only in the difference of the sine and cosine values of the angle between them, therefore, if the angle between the vectors is such that both its sine and cosine values are equal, the magnitudes of the scalar and vector product of such vectors will also be equal. Now, 45⁰ is the angle whose sine = cosine = 1/√2, therefore, if two vectors are making 45⁰ angle between them, the magnitudes of the scalar and vector products of such vectors will be equal. Here in this case,
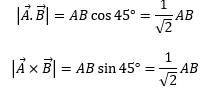
What is the torque acting on the wheel of radius 2 m?

(A)10 N clockwise (B) 10 N m anticlockwise (C) 10 N m clockwise (D) 5 N m clockwise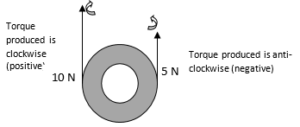

Solution Hint: The force 10 N is producing a clockwise torque. Take it as negative. The 5 N force is producing anti-clockwise torque. Take it positive. Apply the formula and find both torques. Then add them. Remember the anti-clockwise torque is positive. Θ in both cases is 90^o.

Multiple Choice Questions, Vectors and Equilibrium

7 Comments

Leave a Reply Cancel reply

Contact Us