Question 4: What do rectangular components mean? Explain addition of vectors by rectangular components.

Answer

Rectangular components

Replacing a vector by two or more than two vectors is called the resolution of vectors. The vectors so obtained are called the components of the original vector. If the components of the vector are mutually perpendicular then they are called the rectangular components of the original vector.

Addition of vectors by rectangular components

Addition of vectors by rectangular components, sometimes called the analytical method of vector addition, is yet another method by which vectors can be added. This method gives more accurate results than the graphical or head-to-tail method because it is more mathematical and free from the possible errors of measurements and the never-perfect drawings.

Suppose we add two vectors and by the method of addition of rectangular components and let their resultant is , which in the given figure,  makes an angle θ with the x-direction.

First, we add and   geometrically. Place the tail of at the tip of and join the tail of   to the head of .

Resultant vector = OB =   ——-        (A)

Second, we add the same two vectors by rectangular components.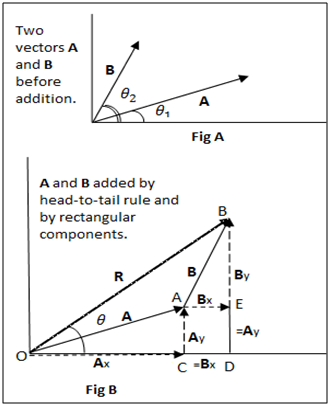
Draw perpendicular from the tip of  on x-axis which meets at point C. A_x and A_y are the x- and y-components of .

x-component of = A_x = OC———–  (i)
y-component of  = A_y = CA = DE —– (ii)

Since A_x and A_y are perpendicular to one another and their resultant is , therefore, they are rectangular components of .

Now draw perpendicular from point B on x-axis at D.
It is clear from the diagram and the rectangular symmetry of the figure that,
x-component of   = B_x = AE = CD ——–    (iii)
y-component of   = B_y = EB ———            (iv)
Since AE and EB are at right angle to each other and their resultant is ; these are the rectangular components of .
Similarly, resolve   in rectangular components by drawing perpendicular from point B on x-axis which meets at point D.
x-component of   = R_x = OD ——— (v)
y-component of   = R_y = DB ———- (vi)
OD and DB are perpendicular to each other, therefore, are rectangular components of .
From the figure, it is clear that,
OD = OC + CD
Substituting values from (v), (i) and (iii) respectively,

R_x = A_x + B_x         ———–                   (vii)

And DB = DE + EB
Substituting values from (vi), (ii) and (iv),

R_y = A_y + B_y         ———–             (viii)
R_x and R_y are the rectangular components of  ,

Magnitude of = R_x + R_y

Substituting from (vii) and (viii),
Magnitude of  = ( A_x + B_x) + (A_y + B_y)
Hence generalizing the result, when we add the vectors by their rectangular components, the x-component of the resultant vector is obtained by adding the x-components of the vectors to be added and the y-component is obtained by adding the y-components of all the vectors to be added.
Mathematically,

R_x = A_x + B_x + C_x +        ——-      (P)
R_y = A_y + B_y + C_y +        ——-      (Q)

Magnitude of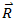 

Magnitude of the resultant vector   is found by applying the Pythagorean Theorem to the right angled triangle OBD in the figure,

Direction of 

Direction of the resultant vector is calculated by,

Where R_x and R_y are calculated from equations (P) and (Q), respectively. Putting the values of R_x and R_y and applying the rules for finding θ in the Cartesian coordinates, the direction of the resultant vector can be found.