Question 6: Define Torque. Explain why it is equal to the vector product of force and moment arm?
Answer:
Definition of torque
Torque is the turning effect produced in a body which is turning about a fixed point due to an applied force.
Mathematically,![]()
Where ![]() is the torque produced,
is the torque produced, ![]() is the applied force and
is the applied force and ![]() is the perpendicular distance between the line of action of force and the pivot.(Pivot is the point about which the body is rotating.)
is the perpendicular distance between the line of action of force and the pivot.(Pivot is the point about which the body is rotating.)
Explanation of torque
The turning effect or torque depends on the following factors.
- Applied force : The turning effect increases when we push the turning body harder and vice versa. So torque is directly proportional to the applied force.
- Moment arm: Moment arm
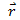 is the perpendicular distance between the force and point of rotation. This is in fact the effective component of the force which produces the torque and depends upon the angle which the force makes with the position vector of the point at which it is applied. Torque is directly proportional to the moment arm.
is the perpendicular distance between the force and point of rotation. This is in fact the effective component of the force which produces the torque and depends upon the angle which the force makes with the position vector of the point at which it is applied. Torque is directly proportional to the moment arm. - Direction of torque: As a vector quantity, torque should also have a direction. The direction of torque is determined by right hand rule. According to this rule, the direction of torque is up if the rotation is in the anti clock-wise direction. The direction of the torque is down if the body is turning in the clock-wise direction. Direction of torque is usually represented by a unit vector
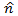 .
.
Thus the proper way of writing torque is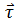 = rFsinθ .
= rFsinθ .
Why Torque = force × moment arm?
As already stated torque depends upon the applied force and moment arm. This is quite clear that an increased force will produce more turning effect or torque and if the force is decreased the turning effect will also decrease. In the same way, increasing the moment arm will also increase the torque and vice versa.
An interesting situation arises with changing the direction of the force. When we gradually change the direction of the force, the torque is also gradually changed. Few situations are hereby depicted in the adjacent fig.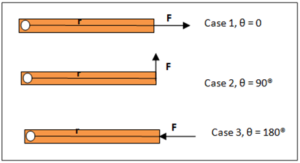
- Force
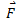 is acting on a rod rotating around the pivot ‘O’.
is acting on a rod rotating around the pivot ‘O’. 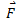 is making an angle θ = 0° with
is making an angle θ = 0° with 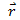 . The line of action of force
. The line of action of force 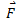 passes through the center of pivot in this case. No turning effect is produced.
passes through the center of pivot in this case. No turning effect is produced. - Now let the direction of force is changed. It acts at an angle 90° with
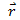 now. It is our common experience that the turning effect is now maximum.
now. It is our common experience that the turning effect is now maximum. - Let the direction of force is further changed. Now the force is making an angle of 180° with the moment arm . We observe the torque is again zero.
To analyze the results of our experiment, we know that sin0° = 0. And when the angle between ![]() and
and ![]() is zero, the torque is also zero.
is zero, the torque is also zero.
The torque is maximum at angle 90°. Sine value is also maximum at this angle.
Torque is again 0 when the angle is 180°. Sine value of the 180° is also zero.
The conclusion is the turning effect or torque is proportional to the sine value of the angle between ![]() and
and ![]() . Therefore, torque is proportional to the magnitude of the force applied, magnitude of moment arm and the sine of the angle between them. Therefore,
. Therefore, torque is proportional to the magnitude of the force applied, magnitude of moment arm and the sine of the angle between them. Therefore,
= rFsinθ
This is exactly what the vector product is. Therefore, ![]()
Thus torque is equal to the vector product of force and moment arm.

Pingback:Comprehensive Questions, Vectors and equilibrium, Physics 11 … msa
Pingback:Vector product, its properties and significance … msa – msa
Pingback:steps-for-solution-of-problems-in-equilibrium – msa