Question 6: Explain vector product of two vectors.
Answer
Definition of Vector or cross Product
A vector product of two vectors is one which yields a vector quantity.
Mathematically,
![]() ×
×![]() = AB sinθ
= AB sinθ![]()
If ![]() and
and ![]() are two vectors to be multiplied vectorally, then their resultant is a vector
are two vectors to be multiplied vectorally, then their resultant is a vector ![]() .
.
The resultant vector is perpendicular to both ![]() and
and ![]() and its magnitude is equal to the product of the magnitudes of
and its magnitude is equal to the product of the magnitudes of ![]() and
and ![]() and the sine of the smaller angle between them. The direction of the resultant vector is determined by right hand rule.
and the sine of the smaller angle between them. The direction of the resultant vector is determined by right hand rule.
This is important to note that unlike dot product, cross product is not commutative. The order of the vectors in the product is important.![]() ×
× ![]() ≠
≠ ![]() ×
× ![]()
Properties of Vector Product
Some of the important properties of the vector product are as follow.
- Vector Product does not obey the Commutative Property.
If and are two vectors then,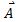 ×
× 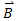 ≠
≠ 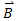 ×
× 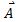
- Vector Product obeys the distributive property.
If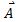 ,
,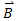 and
and 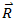 are three vectors, then
are three vectors, then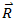 × (
× ( 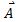 ×
× 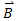 ) = (
) = ( 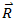 ×
×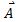 ) + (
) + ( 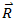 ×
× 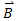 )
) - If
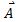 ×
× 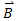 = 0, then either,
= 0, then either,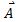 = 0
= 0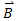 = 0
= 0- both are zero
- Or the angle between them is 0°
Physical significance of Vector Product
Vector product has key importance in the study of Physics. Important physical quantities are determined with the help of vector product.
- Torque is determined with the help of vector product of
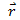 and
and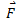 .
. 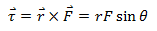
- Angular momentum of a body is determined by vector product.
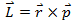
- Area of a parallelogram is determined by the use of vector product. If
 and
and are the adjacent sides of a parallelogram and
are the adjacent sides of a parallelogram and  is its area, then
is its area, then 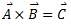
Apart from Mechanics, vector product is also used in other branches of Physics.

Pingback:Comprehensive Questions, Vectors and equilibrium, Physics 11 … msa
Pingback:Explanation o Torque, Physics 11 … msa – msa
Pingback:Explain dot product, dot product of characteristic vectors … msa – msa