Question 5: Define and explain scalar or dot product?
Answer
Definition of scalar product:
Scalar or dot product of two vectors is defined as the product that yields a result that is a scalar quantity.
Mathematically,
![]() .
.![]() = AB cosθ
= AB cosθ
Where θ is the smaller angle between ![]() and
and ![]() .
.
Explanation of scalar product
Let ![]() and
and ![]() are two vectors and θ is the smaller angle between them when placed tail-to-tail. Then the scalar product of the two vectors is;
are two vectors and θ is the smaller angle between them when placed tail-to-tail. Then the scalar product of the two vectors is;![]() .
.![]() = AB cosθ.
= AB cosθ.
Geometrically, it is the product of the magnitude of ![]() and the projection of
and the projection of ![]() on
on![]() . Here ‘A’ is the magnitude of
. Here ‘A’ is the magnitude of ![]() and ‘B’ is the magnitude of
and ‘B’ is the magnitude of![]() . Similarly, cosθ is a number. Therefore, the product is simply the multiplication of three real numbers. As the product of real numbers is commutative (commutation means the order is irrelevant and we can multiply them in any order), therefore, the scalar product is also commutative.
. Similarly, cosθ is a number. Therefore, the product is simply the multiplication of three real numbers. As the product of real numbers is commutative (commutation means the order is irrelevant and we can multiply them in any order), therefore, the scalar product is also commutative.![]() .
. ![]() =
=![]() .
.![]()
Work, flux etc are the examples of scalar product.
Dot product of some characteristic vectors
Since dot product depends on the angle between the two vectors, therefore, some vectors yield interesting results.
- The angle between two parallel vectors is zero. Parallel vectors are when scalarly multiplied the resultant is equal to the product of magnitude of the two vectors.
Let and are parallel, then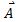 .
. 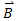 = AB cosθ
= AB cosθ
Since θ = 0 in case of parallel vectors, therefore, cosθ = cos0 = 1. Therefore,
![]() .
.![]() = AB
= AB
In case of unit vectors along the coordinate axes,
![]() Note that the magnitudes of all unit vectors are 1 and cos 0 is also 1.
Note that the magnitudes of all unit vectors are 1 and cos 0 is also 1.
- The angle between two orthogonal vectors is 90°. The product of two orthogonal vectors is, therefore, 0.
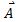 .
.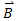 = AB cos90° = 0
= AB cos90° = 0
In case of unit vectors along the coordinate axes
![]()
- The angle between two anti-parallel vectors is 180°. The product of two anti-parallel vectors is, therefore, negative and equal to the product of the magnitudes of the two vectors.
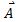 .
.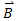 = AB cos180° = AB (-1) = -AB
= AB cos180° = AB (-1) = -AB

Pingback:Comprehensive Questions, Vectors and equilibrium, Physics 11 … msa
Pingback:Explanation o Torque, Physics 11 … msa – msa
Pingback:Vector product, its properties and significance … msa – msa
Pingback:Rectangular components, addition of vectors by rectangular components … msa – msa